Question

Let $f\left(x\right)=1+4x-x^2,\forall x\in R$
$g\left(x\right)=max\{f\left(t\right),x\le t\le (x+1),0\le x<3\}=min\{(x+3),3\le x\le 5\}$ Verify conntinuity of g(x), for all $x\in [0,5]$

Explanation

`f(x)=x^(3)-3x^(2)+6`
If `f'(x)=3x^(2)-6x=0`, then `x=0, 2` are the critical points of `f(x)`.
`x=0` is the point of local maxima and x=2 is the point of local minima.
Clearly, `f(x) ` is increasing in `(-oo,0)` and `(2, oo)` and decreasing in (0,2).

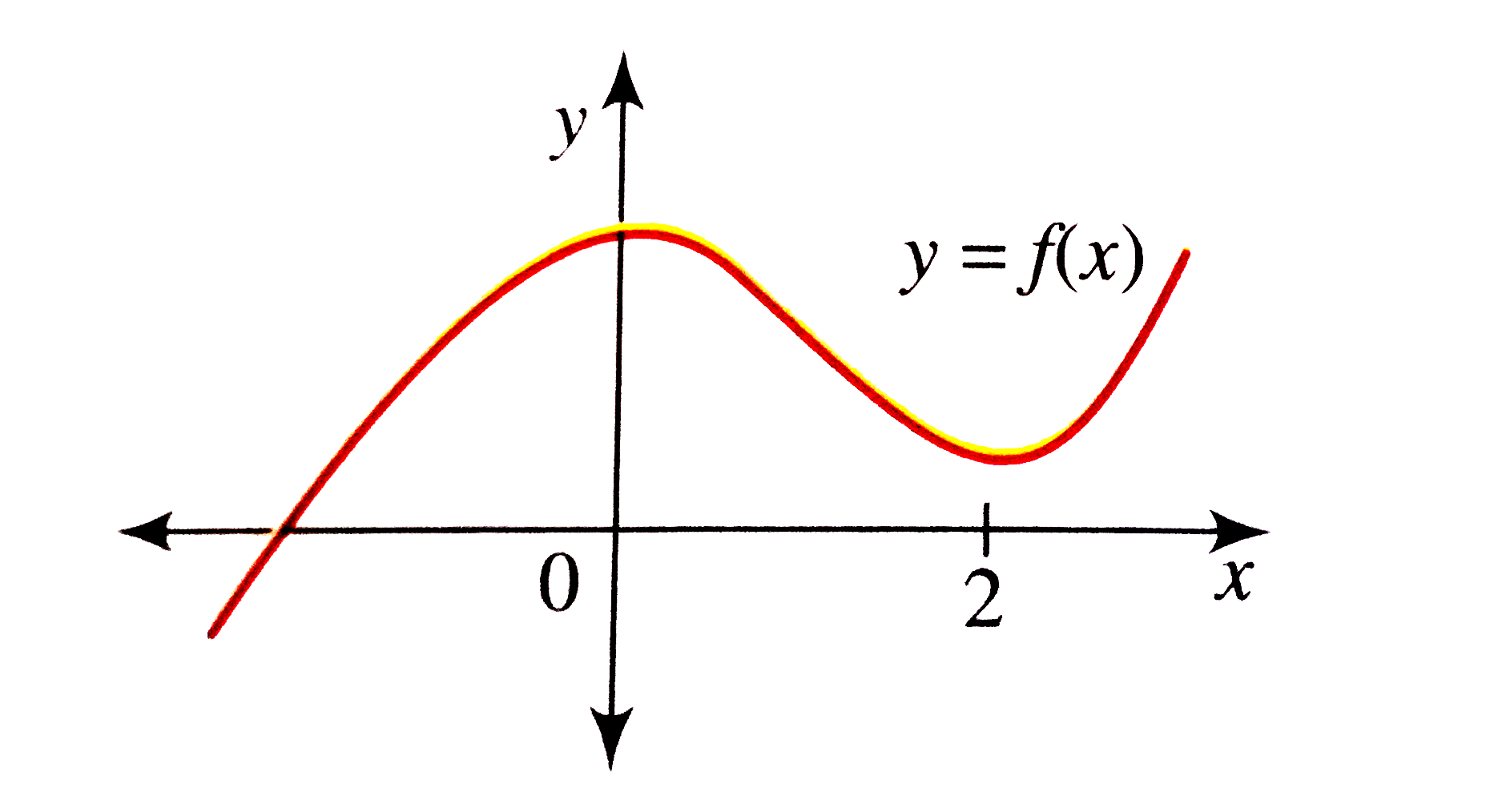
Case 1 : ` x+2 le 0 rArr x le -2`
`rArr " " g(x)=f(x+2), -3 le x le -2`
Case 2: `x+1 lt 0 ` and `0 lt x+2 lt 2`
`x lt -1 ` and `-2 lt x lt 0`
i.e., `-2 lt x lt -1 " " :. g(x)=f(0)`
Case 3: `0 le x+1, x+2 le 2`
`rArr -1 le x le 0, g(x)=f(x+1)`
`rArr g(x)={{:(f(x+2)", " -3 le x lt -2),(f(0)", " -2le x lt -1),(f(x+1)", " -1 le x lt 0),(1-x ", "0 lexlt1):}`