Draw the graph of f(x)=1x2−2x+2.
Video Solution
Text Solution
f(x)=1x2−2x+2
=1(x−1)2+1>0,∀x∈R
f(0)=1, hence the graph intersects the y-axis at (0,1).
f(x)≠0 for any real x, hence the graph never intersects the x-axis.
Further x2−2x+2≠0 for any real x, hence the function has no verical asymptote.
Also the degree of the denominator is higher than the degree of the numerator, hence the graph has horizontal tangent x = 0.
f'(x)=2x−2(x2−2x+2)2
f'(x)=0∴x=1, which is the point of maxima.
For x∈(−∞,1),f(x) increases and for x∈(1,∞),f(x) decreases.
Also f(1)=1
From the above discussion, the graph of the function is shown in the following figure.
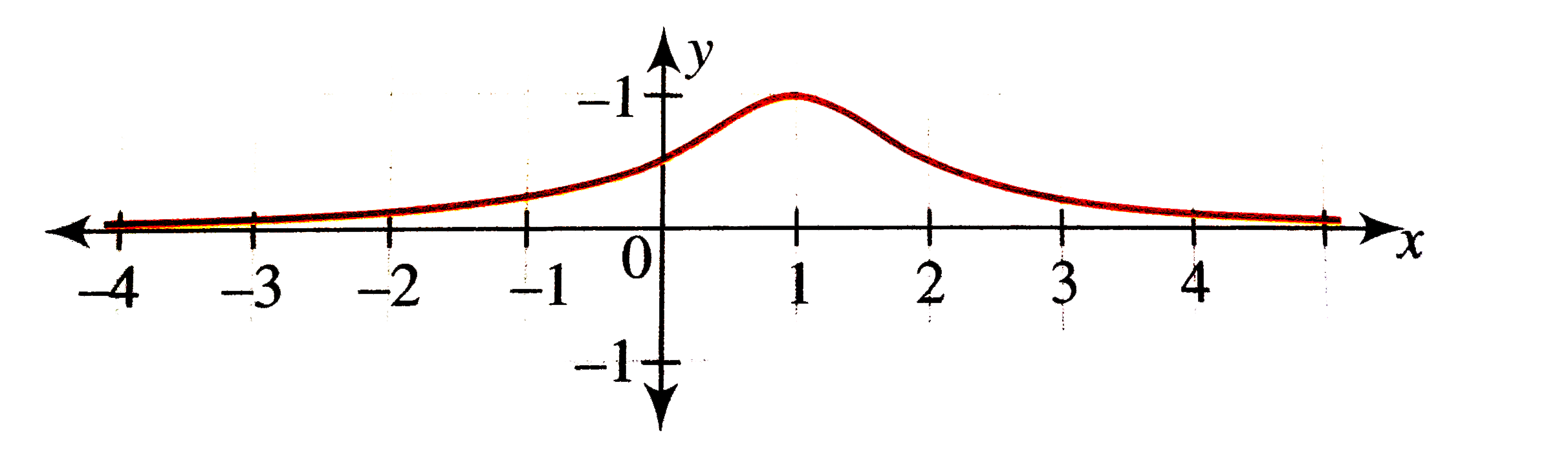
Since f(1−x)=f(1+x), the graph is symmetrical about the line x = 1.
|
Topper's Solved these Questions
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
17 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - CENGAGE ENGLISHCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - ILLUSTRATION
78 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGE ENGLISHCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES
34 Videos
Similar Questions
Draw the graph of y=f(x)=x+1x2+1
View SolutionDraw the graph of y=1x2.
View SolutionDraw the graph of y=2x.
View SolutionDraw the graph of y=(x−1)(x2−x+1).
View SolutionDraw the graph of f(x)=2|x−1|x2+1.
View SolutionDraw the graph of f(x)=x2−5x+6x2−x
View SolutionDraw the graph of y=sin−1(x2)
View SolutionDraw the graph of f(x)=∣∣∣x2−2x2−1∣∣∣ .
View SolutionDraw the graph of f(x)=∣∣∣x2−2x2−1∣∣∣ .
View SolutionDraw the graph of y=f(x)=x2x2+1.
View Solution
