Match the following lists (where represents the greatest integer function) and then choose the correct code.
![Match the following lists (where [x] represents the greatest integer function) and then choose the correct code. Codes : {:(,](https://d10lpgp6xz60nq.cloudfront.net/physics_images/CEN_CAL_C02_E12_005_Q01.png)
Codes :
The correct Answer is:
a.
b.
So limit does not exist.
c.
R.H.L.
Limit does not exist
Topper's Solved these Questions
- LIMITSBOOK - CENGAGE ENGLISHCHAPTER - LIMITSEXERCISE - Numerical Value Type
26 Videos
- LIMITSBOOK - CENGAGE ENGLISHCHAPTER - LIMITSEXERCISE - Archives JEE MAIN
8 Videos
- LIMITSBOOK - CENGAGE ENGLISHCHAPTER - LIMITSEXERCISE - Linked Comprehension Type
20 Videos
- JEE 2019BOOK - CENGAGE ENGLISHCHAPTER - JEE 2019EXERCISE - Chapter 10
9 Videos
- LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSBOOK - CENGAGE ENGLISHCHAPTER - LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSEXERCISE - DPP 1.2
10 Videos
Similar Questions
limx→∞3x[x4]=pq where [.] denotes greatest integer function), then p+q (where p,q are relative prime) is:
View SolutionConsider
∫x3+3x2+2x+1√x2+x+1dx
=(ax2+bx+c)√x2+x+1+λ∫dx√x2+x+1
Now, match the following lists and then choose the correct code.

Codes:
abcd(1)qpsr(2)spqr(3)rqps(4)qspr
View SolutionMatch the duals of the statements in List - I :
List - IList - II(1)(p∨q)∨r(a)(p∨q)∨r(2)(p∧q)∧r(b)(p∧q)∨(r∧s)(3)(p∨q)∧(r∨s)(c)(p∧q)∧r
The correct match is :
View SolutionMatch the columns and choose correct options.
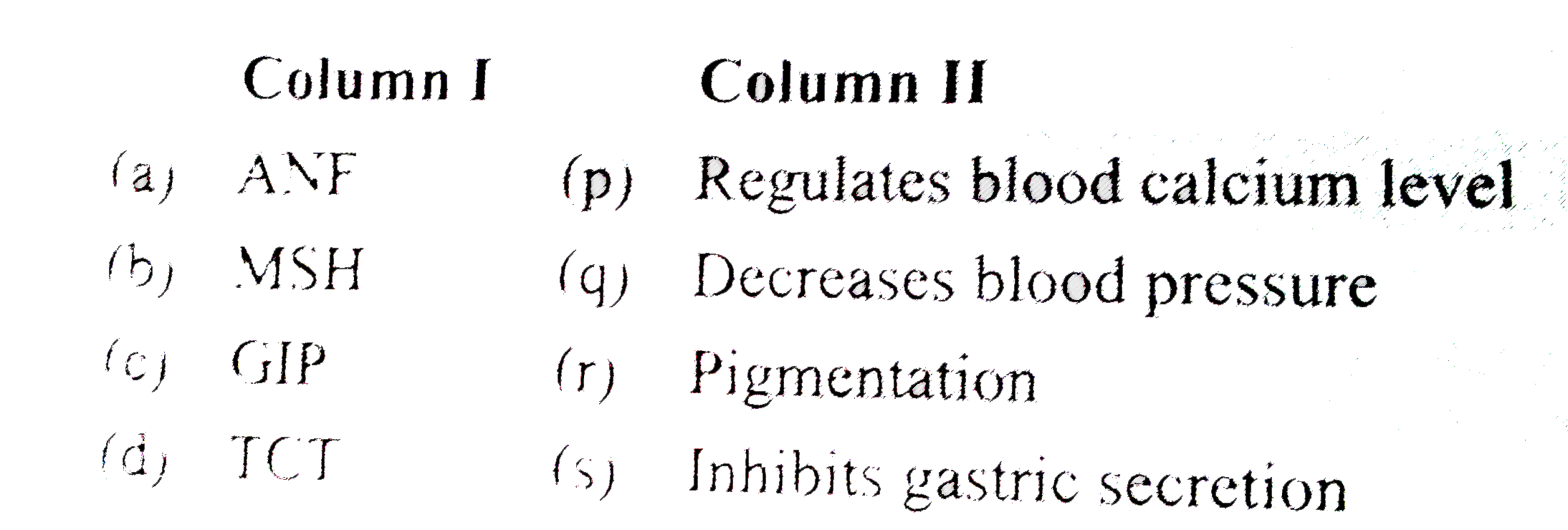
(1) a-q, b-r, c-s, d-p
(2) a-s, b-p, c-q, d-r
(3) a-q, b-p, c-s, d-r
(4) a-s, b-p, c-r, d-q
View SolutionMatch the coloumn

A→QB→RC→PD→SA→QB→RC→SD→PA→RB→QC→SD→PA→RB→QC→PD→S
View SolutionThe mean of is same as the mean of Then which of the following is correct? p=q=r (b) q=r=s q=r (d) p=r+s
View SolutionIf p+q+r=0=a+b+c, then the value of the determinant ∣∣ ∣ ∣∣paqbrcqcrapbrbpcqa∣∣ ∣ ∣∣is (a)0 (b) pa+qb+rc (c) 1 (d) none of these
View SolutionConstruct the truth table for the followings statements :
(a) (p∧q)→~p (b)(p∧q)→(p∨q)
(c) (p∧q)→r (d)[p∧(~r)]→(q∨r)
View SolutionMatch the duals of the statements in list - I :
List - IList - II(a)(p∧q)∨t(I)(p∧q)∧t(b)(p∨t)∧r(II)(p∨q)∧t(c)(p∨q)∨t(III)(p∧t)∨r
The correct match is :
View SolutionIf PQRS is a square, then write the measure of ∠SRP
View Solution
