Consider
∫x3+3x2+2x+1√x2+x+1dx
=(ax2+bx+c)√x2+x+1+λ∫dx√x2+x+1
Now, match the following lists and then choose the correct code.

Codes:
abcd(1)qpsr(2)spqr(3)rqps(4)qspr
The correct Answer is:4
∫x3+3x2+2x+1√x2+x+1dx
=(ax2+bx+c)√x2+x+1+λ∫dx√x2+x+1
Differentiating both side, we get
x3+3x2+2x+1√x2+x+1=(ax2+bx+c)(2x+1)2√x2+x+1+(2ax+b)√x2+x+1+λ1√x2+x+1
=6ax3+(5a+4b)x2+(4a+3b+2c)x+(c+2b+2λ)2√x2+x+1
Now, compare coefficients on both sides and solve equations.
Topper's Solved these Questions
- INDEFINITE INTEGRATIONBOOK - CENGAGE ENGLISHCHAPTER - INDEFINITE INTEGRATIONEXERCISE - EXERCISES (Numerical Value Type)
10 Videos
- INDEFINITE INTEGRATIONBOOK - CENGAGE ENGLISHCHAPTER - INDEFINITE INTEGRATIONEXERCISE - Archives JEE MAIN (Single Correct Answer Type)
7 Videos
- INDEFINITE INTEGRATIONBOOK - CENGAGE ENGLISHCHAPTER - INDEFINITE INTEGRATIONEXERCISE - Exercises (Linked Comprehension Type)
17 Videos
- HYPERBOLABOOK - CENGAGE ENGLISHCHAPTER - HYPERBOLAEXERCISE - COMPREHENSION TYPE
2 Videos
- INEQUALITIES AND MODULUSBOOK - CENGAGE ENGLISHCHAPTER - INEQUALITIES AND MODULUSEXERCISE - Single correct Answer
21 Videos
Similar Questions
Match the following lists (where [x] represents the greatest integer function) and then choose the correct code.
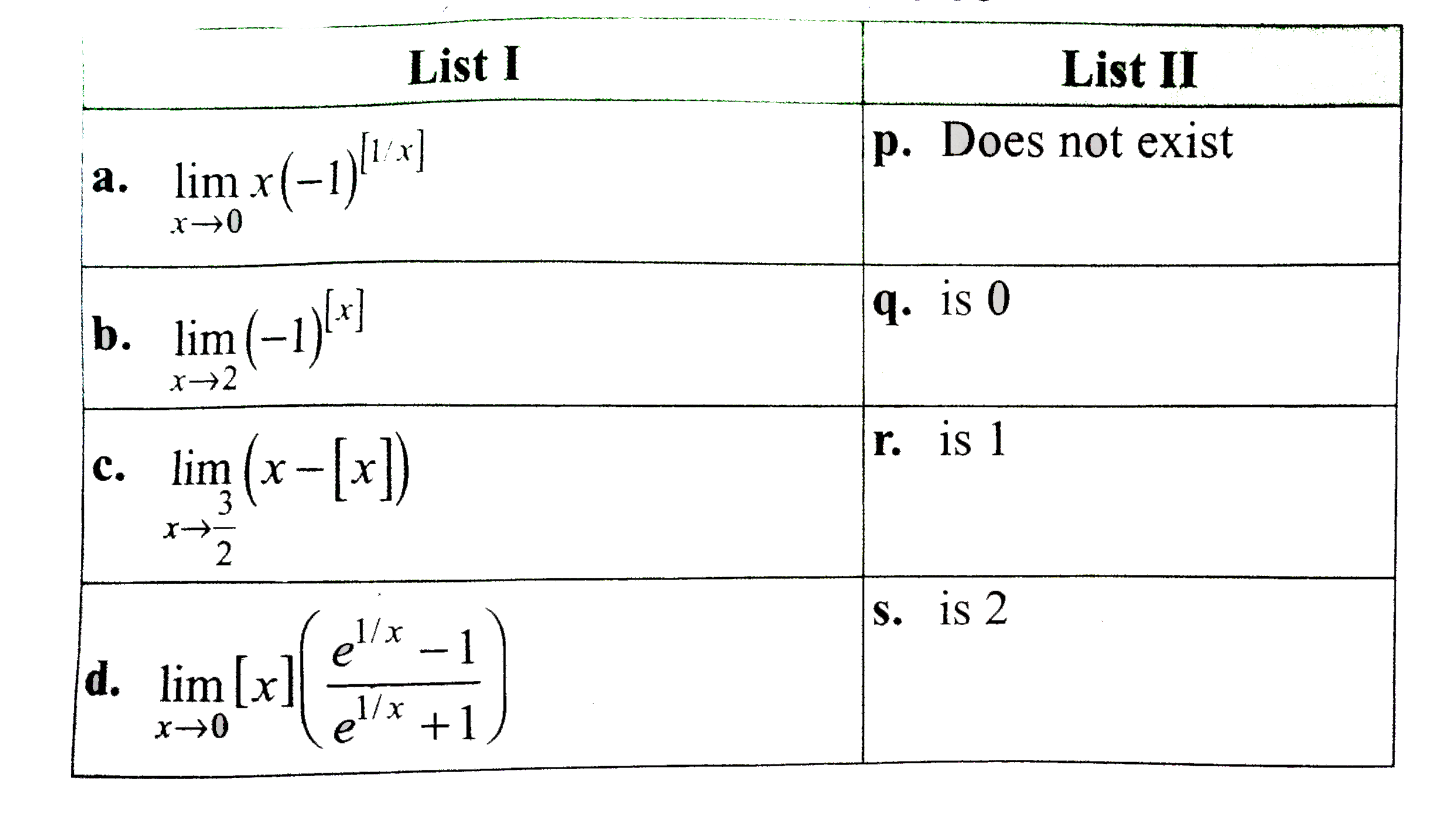
Codes :
a b c d(1)s r q p(2)q p s p(3)s r p q(4)p p q r
View SolutionIf ∫x+(cos−13x)2√1−9x2dx=P√1−9x2+Q(cos−13x)3+c then
View SolutionMatch List - I and List - II .
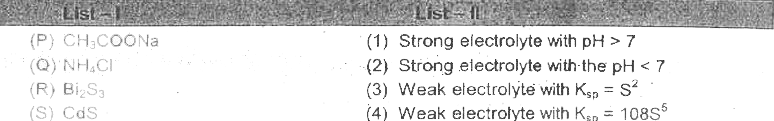
PQRS(A)4312(B)3421(C)4321(D)4231
View SolutionMatch List - I and List - II .

PQRS(A)4213(B)4132(C)1423(D)4123
View SolutionEvaluate: ∫dx(x−p)√(x−p)(x−q)
View SolutionMatch the columns and choose correct options.
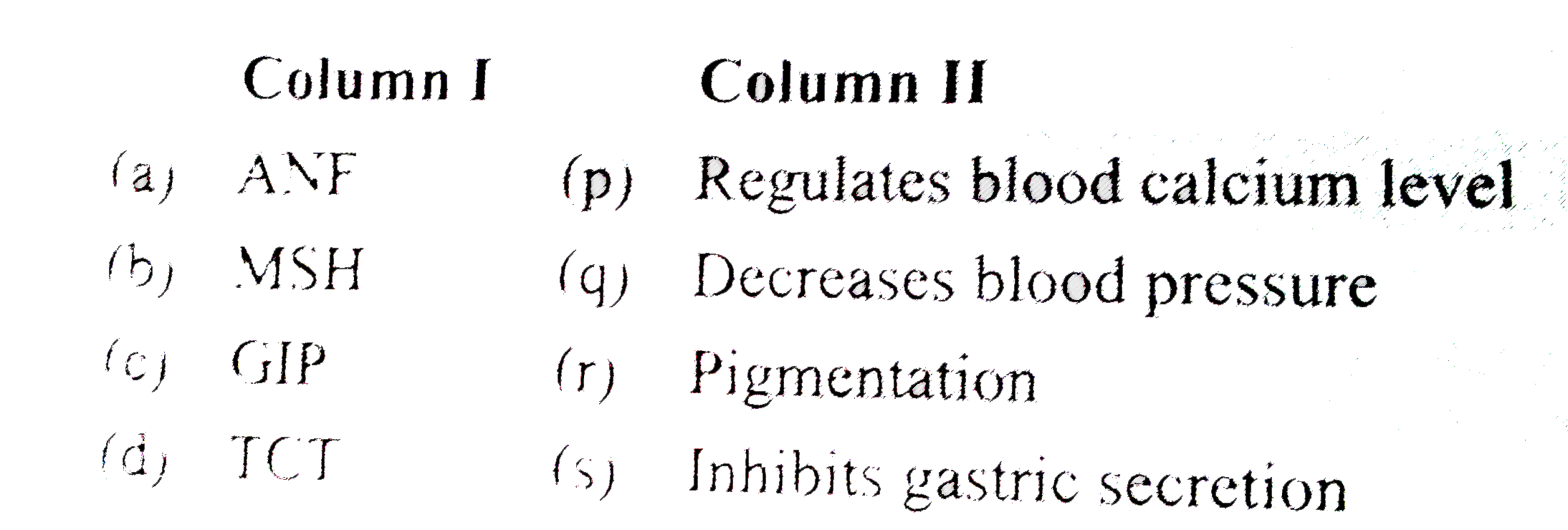
(1) a-q, b-r, c-s, d-p
(2) a-s, b-p, c-q, d-r
(3) a-q, b-p, c-s, d-r
(4) a-s, b-p, c-r, d-q
View SolutionDifferentiate w.r.t x
√x(2x+3)2/√x+1
View SolutionLet a, b, c be non zero numbers such that
∫30√x2+x+1(ax2+bx+c)dx=∫50√1+x2+x(ax2+bx+c)dx. Then the quadratic equation ax2+bx+c=0 has
View SolutionDifferentiate the following function with respect of x:ax+bpx2+qx+r
View SolutionDifferentiate the following function with respect of x:px2+qx+rax+b
View Solution
