Lines L1≡ax+by+c=0 and L2≡lx+my+n=0 intersect at the point P and make an angle θ with each other. Find the equation of a line different from L2 which passes through P and makes the same angle θ with L1.

From the figure. Image of point P(h,k) on required line in the line L1 lies on line L2.
So, equation of required line is locus of point P such that its image in line L1 lies on line L2.
Let image of point P in line L1 be Q(x1,y1).
⇒x1−ha=y1−kb=2(ah+bk+c)a2+b2
⇒x1=−2a(ah+bk+c)a2+b2+h
and y1=−2b(ah+bk+c)a2+b2+k
Now ,Q(x1,y1)lies on the lineL2.
∴l[−2a(ah+bk+c)a2+b2+h]+m[−2b(ah+bk+c)a2+b2+k]+n=0
Therefore, equation of required line is
2(al+mb)(ax+by+c)−(a2+b2)(lx+my+n)=0
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXAMPLE12videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - CONCEPT APPLICATION EXERCISE 2.123videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
lines L1:ax+by+c=0 and L2:lx+my+n=0 intersect at the point P and make a angle θ between each other. find the equation of a line Ldifferent from L2 which passes through P and makes the same angle θ with L1
View SolutionFind the equation of the straight line through the point (α,β) and perpendiculasr to the line lx+my+n=0.
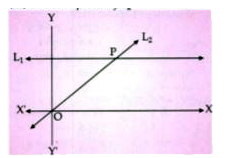
View SolutionGiven equation of line L1 is y=4
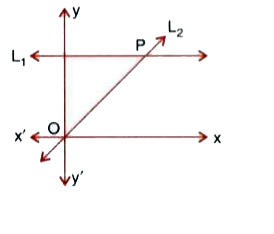
Write the slope of line L1 if L2 is the bisector of angle O.View SolutionTwo lines l and m interset at the O and P is Point on a line n Passing through the point O such that P is equidistant from l and m. Prove that n is the bisectof the angle formed by l and m
View SolutionThe equation of line l1 is y=2x+3, and the equation of line l2 is y=2x-5.
View Solution(i) Find the equation of line passing through (2,2) and makes an angle of 135∘ from positive direction of X-axis.
(ii) Find the equation of a line passing through the point (2,1) and makes an angle 'θ' from the positive direction of X-axis where cosθ=−13.View Solutionthe lines L1 and L2 denoted by 3x2+10xy+8y2+14x+22y+15=0 intersect at the point P and have gradients M1 and M2 respectively.The acute angles between them is θ . which of the following relations hold good ?
View SolutionThe direction cosines of the lines bisecting the angle between the line whose direction cosines are l1,m1,n1andl2,m2,n2 and the angle between these lines is θ, are
View SolutionGiven equation of line L1 is y = 4 and line L2 is the bisector of angle O.
Write the coordinates of point P.
 View Solution
View SolutionIn Fig. 30, lines l1 and l2 intersect at O, forming angles as shown in the figure. If x=450, find the values of y,z and u.
View Solution

