Question

The equations of bisectors of two lines $L_1\&L_2$ are $2x-16y-5=0$ and $64x+8y+35=0$. lf the line $L_1$ passes through $(-11,4)$, the equation of acute angle bisector of $L_1$ & $L_2$ is:

Explanation

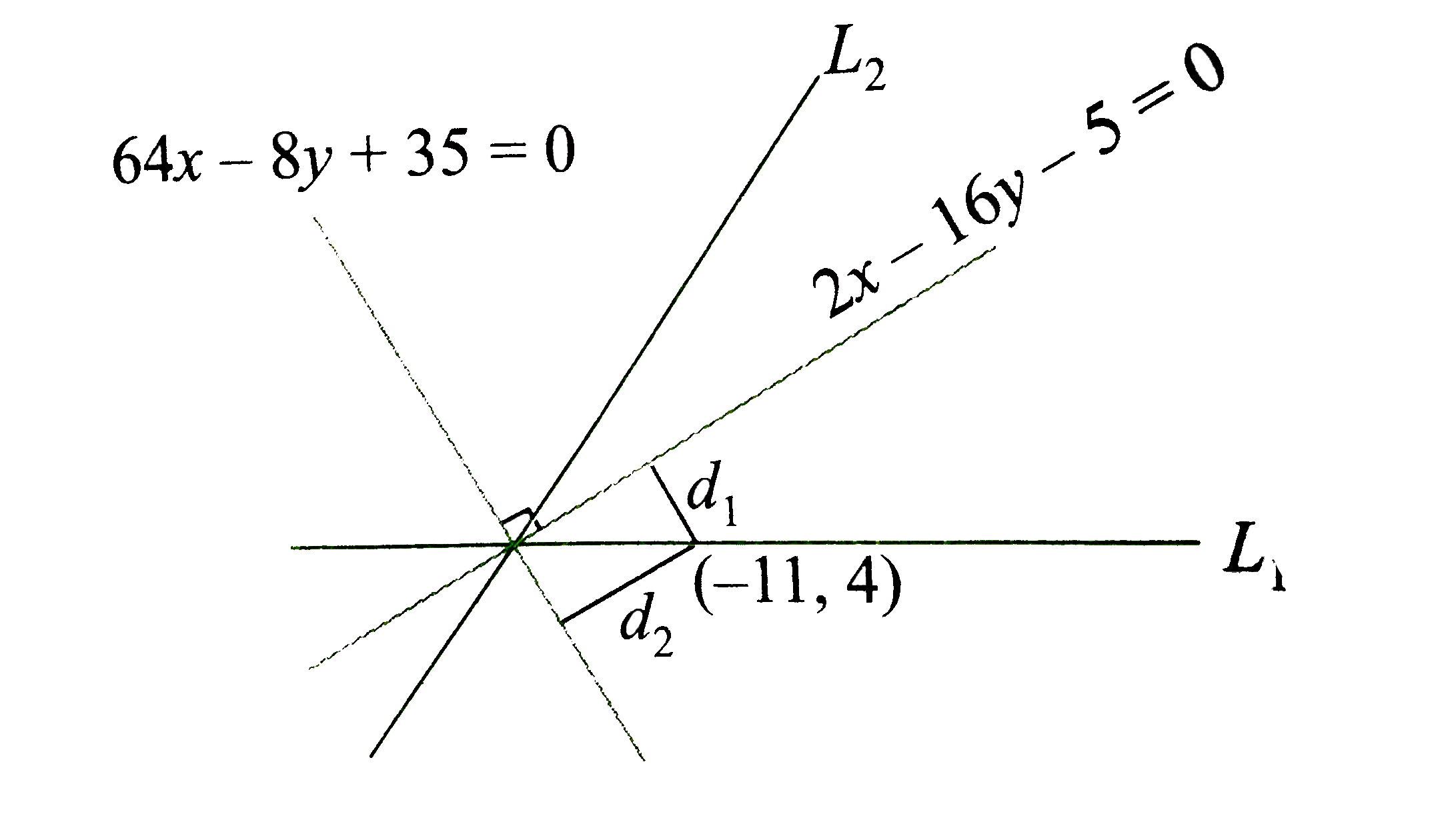
From the figure,
`d_(1) = (|2(-11)-16(4)-5|)/(sqrt(4+256)) = (91)/(2sqrt(65)) ~= 5.6 " " (1)`
`d_(2) = (|64(-11)+8(4)+35|)/(sqrt((64)^(2)+8^(2))) = (637)/(64.49) ~= 9.87 " " (2)`
`d_(1) lt d_(2)`
Therefore, 2x-16y-5=0 is acute angle bisector and 64x+8y+35=0 is obtuse angle bisector.