Question

The line 6x+8y=48 intersects the coordinates axes at A and B, respecively. A line L bisects the area and the perimeter of triangle OAB, where O is the origin.
Line L

Options

A. does not intersect AB
B. does not intersect OB
C. does not intersect OA
D. can intersect all the sides

Answer

C

Explanation

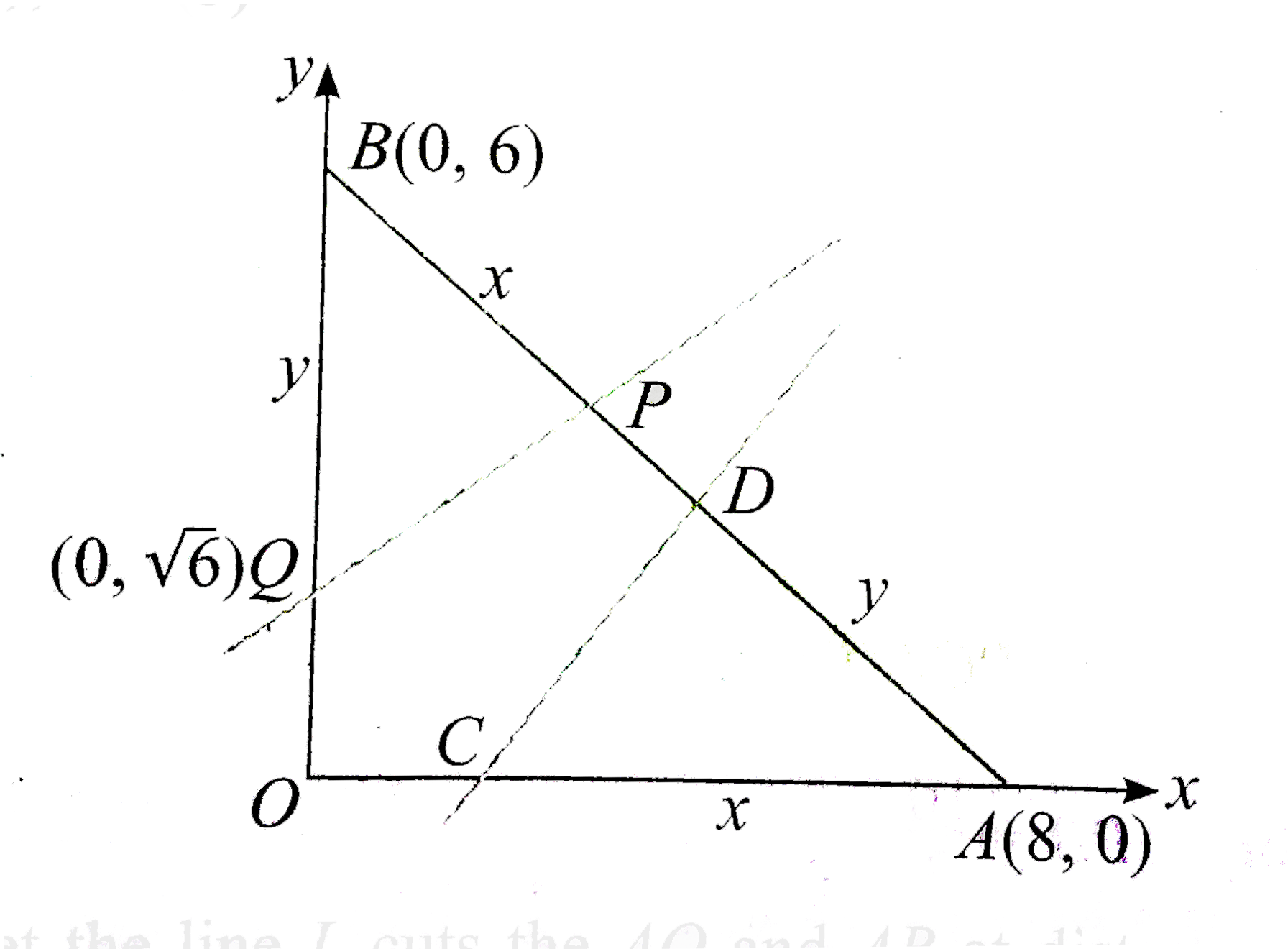
Case I : Let the line L cuts the AO and AB at distances x and y, respectively, from A. Then, the area of the triangle with sides x and y is
`(1)/(2)xy" sin"(angleCAD) = (1)/(2) * xy * (3)/(5) = (3xy)/(10) = 12`
or xy=40
Also, x+y=12 (from perimeter bisection). Then x and y are the roots of `r^(2)-12x+40=0` which has imaginary roots.
Case II: if the line L cuts OB and BA at distances y and x, respectively, from B, then we have xy=30 and x+y=12.
Solving, we get `x=6+sqrt(6) " and " y=6-sqrt(6).`
Case III: If the line L cuts the sides OA and OB at distances x and y, respectively, from O, then
x+y=12 and xy=24
`therefore x,y = 6+-2sqrt(3)` (not possible)
So there is a unique line possible. Let point P be `(alpha, beta)`.
Using the parametric equation of AB, we have
`beta = 6-(3)/(5)(6+sqrt(6))`
`"and " alpha = (4)/(5)(6+sqrt(6))`
Hence, the slope of PQ is
`(beta-sqrt(6))/(alpha-0) = (10-5sqrt(6))/(10)`