ABCD is a parallelogram. x + 2y = 3 and 2x + y = 3 are the equations of the diagonals AC and BD respectively. AC = 4 units and area of parallelogram ABCD is 8 sq. units then The length of BC is equal to
√232/3
4√58/9
3√58/9
4√58/9
The correct Answer is:A
cos(π−θ)=AP2+PB2−AB22AP×PB
or −45=4+(100/9)−AB22×2×(10/3)
or Bc=√2323
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MATRIX MATCH TYPE)
8 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (NUMERICAL VALUE TYPE)
13 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWERS TYPE)
30 Videos
- STRAIGHT LINEBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )
1 Videos
Similar Questions
Let ABCD be a parallelogram the equation of whose diagonals are AC:x+2y=3; BD:2x+y=3. If length of diagonal AC=4 units and area of ABCD=8 sq. units. Then
(i) The length of the other diagonal is
(ii) the length of side AB is equal to
View SolutionLet ABCD be a parallelogram the equation of whose diagonals are AC:x+2y=3; BD: 2x + y = 3. If length of diagonalAC=4 units and area of ABCD=8 sq. units. Find the length of the other diagonal is a. 10/3 b. 2 c. 20/3 d. None of these
View Solution
Knowledge Check

In parallelogram ABCD above, AC=3 and AD=5. What is the area of ABCD?A12B15C18D20
Given a parallelogram ABCD where X and Y are the mid-points of the sides BC and CD respectively . Prove that:
ar (ΔAXY)=38×ar(/gm)ABCD
View SolutionABCD is a parallelogram where A (x, y), B (5, 8), C (4, 7) and D 2, -4). Find
(ii) Equation of diagonal BD.
View SolutionIn a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=12(AB−CD).

View SolutionIn a !ABC the length of the median AD to the side BC is 4 units. If ∠A=60∘ and the area of the triangle is 2√3 sq. units. The length of side BC, is
View SolutionIn a parallelogram as shown in the figure (a≠b)
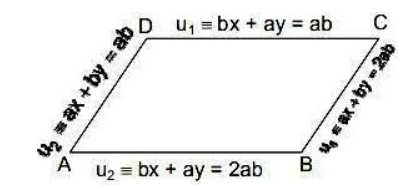
Prove that the equation of the diagonal AC is (a+b)x+(a+b)y=3ab
View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides BC and AD respectively. Show that the line segment BF and ED trisect the diagonal AC.
View SolutionL and M are the mid-points of sides AB and DC respectively of parallelogram ABCD. Prove that segments DL and BM trisect diagonal AC.
View Solution
