If adjB=A,|P|=|Q|=1,thenadj(Q−1BP−1) is PQ b. QAP c. PAQ d. PA1Q
PQ
QAP
PAQ
PA−1Q
The correct Answer is:C
To solve the problem, we need to find the adjoint of the matrix expression Q−1BP−1 given that adj(B)=A and |P|=|Q|=1.
1. Write the expression for the adjoint:
adj(Q−1BP−1)=adj(P−1)⋅adj(B)⋅adj(Q−1)
2. Use the property of adjoint for inverses:
The property states that:
adj(A−1)=adj(A)|A|
Applying this to P−1 and Q−1:
adj(P−1)=adj(P)|P|andadj(Q−1)=adj(Q)|Q|
3. Substituting the determinants:
Since |P|=1 and |Q|=1, we have:
adj(P−1)=adj(P)andadj(Q−1)=adj(Q)
4. Substituting the adjoint of B:
We know from the problem statement that adj(B)=A. Thus, we can substitute:
adj(Q−1BP−1)=adj(P)⋅A⋅adj(Q)
5. Final expression:
We can write the final expression as:
adj(Q−1BP−1)=PAQ
Conclusion:
The answer is PAQ.
adj(Q−1BP−1)=adj(P−1)⋅adj(B)⋅adj(Q−1)
The property states that:
adj(A−1)=adj(A)|A|
Applying this to P−1 and Q−1:
adj(P−1)=adj(P)|P|andadj(Q−1)=adj(Q)|Q|
Since |P|=1 and |Q|=1, we have:
adj(P−1)=adj(P)andadj(Q−1)=adj(Q)
We know from the problem statement that adj(B)=A. Thus, we can substitute:
adj(Q−1BP−1)=adj(P)⋅A⋅adj(Q)
We can write the final expression as:
adj(Q−1BP−1)=PAQ
The answer is PAQ.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - MATRICESEXERCISE - Multiple Correct Answer49videos
MATRICES
- BOOK - CENGAGE ENGLISHCHAPTER - MATRICESEXERCISE - Linked Comprehension Type27videos
MATRICES
- BOOK - CENGAGE ENGLISHCHAPTER - MATRICESEXERCISE - CAE 13.517videos
MATRICES
- BOOK - CENGAGE ENGLISHCHAPTER - MATHMETICAL REASONINGEXERCISE - Archives10videos
MATHMETICAL REASONING
- BOOK - CENGAGE ENGLISHCHAPTER - METHODS OF DIFFERENTIATIONEXERCISE - Single Correct Answer Type46videos
METHODS OF DIFFERENTIATION
Similar Questions
If adjB=A,|P|=|Q|=1,then.adj(Q−1BP−1) is a.PQ b. QAP c. PAQ d. PA−1Q
View SolutionIf P is a non-singular matrix, with (P−1) in
terms of 'P', then show that adj(Q−1BP−1)=PAQ . Given
that (B)=Aand|P|=|Q|=1.View SolutionIf P is an orthogonal matrix and Q=PAPTandx=PTQ1000P then x−1 is , where A is involutary matrix. A b. I c. A1000 d. none of these
View SolutionIn Figure, if quadrilateral PQRS circumscribes a circle, then PD+QB= (a)PQ (b) QR (c) PR (d) PS
View SolutionIf ABC≅PQR and ABC is not congruent to RPQ, then which of the following not true: (a)BC=PQ (b) AC=PR (c) AB=PQ (d) QR=BC
View SolutionIf in an A.P., the pth term is q and (p+q)th term is zero then the qth term is
a.−p b. p c. p+q d. p−qView SolutionABCD is a parallelogram. P is a point on AD such that AP=13 AD and Q is a point on BC such that CQ=13BC. Prove that AQCP is a parallelogram.
View SolutionIn a right triangle ABC right-angled at B, if PandQ are points on the sides ABandAC respectively, then (a)AQ2+CP2=2(AC2+PQ2) (b)2(AQ2+CP2)=AC2+PQ2 (c)AQ2+CP2=AC2+PQ2 (d)AQ+CP=12(AC+PQ).
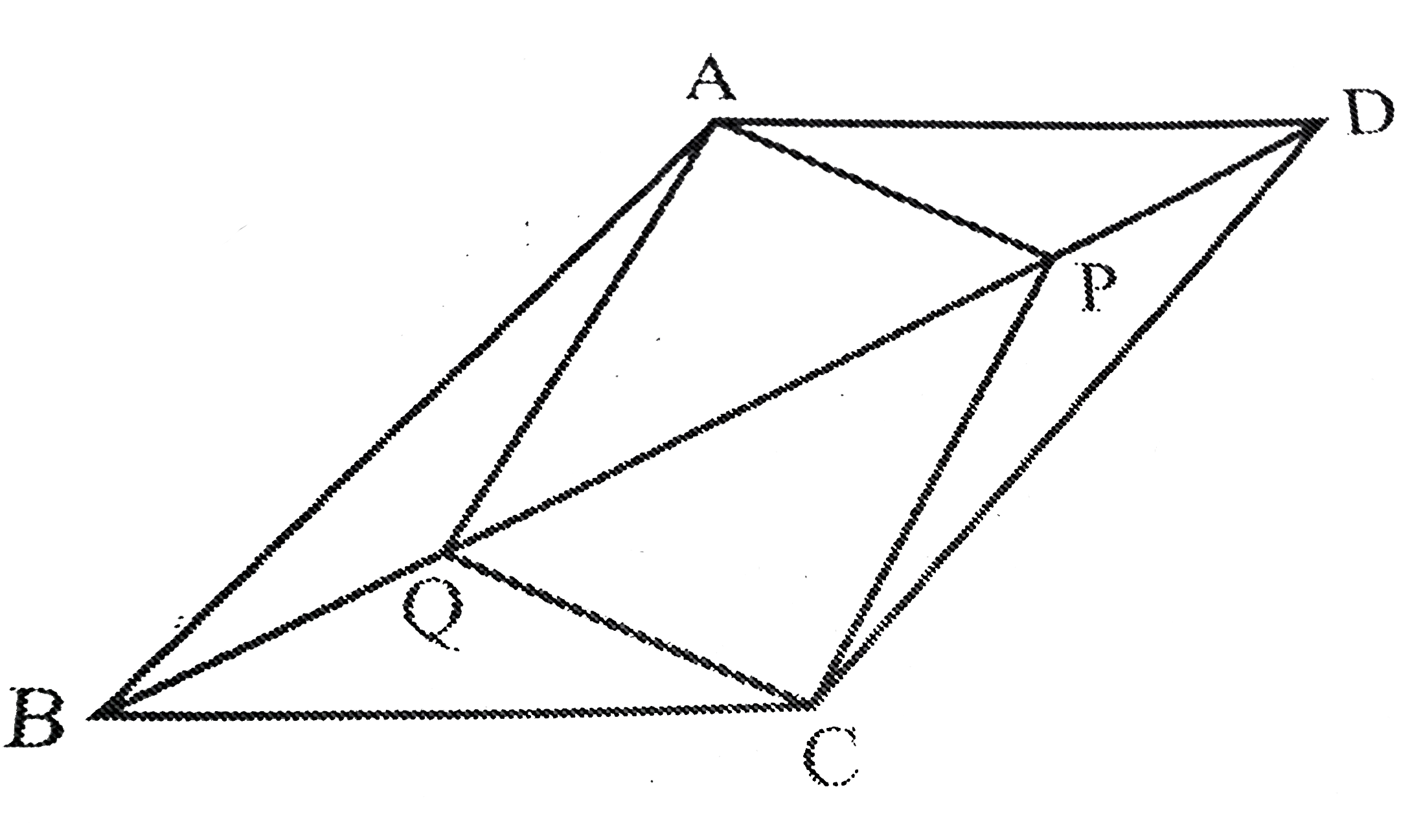
View SolutionIn parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ. Show that:
(i) ΔAPD≅ΔCQB
(ii) AP=CQ
(iii) ΔAQB≅ΔCPD
(iv) AQ=CP
(v) APCQ is a parallelogram.
 View Solution
View SolutionIf ΔPQR ≅ΔEFD, then ∠E=
(a) ∠P
(b) ∠Q
(c) ∠R
(d) None of theseView Solution

