Two rods are rotating about two fixed points in opposite directions. If they start from their position of coincidence and one rotates at the rate double that of the other, then find the locus of point of the intersection of the two rods.
To find the locus of the point of intersection of two rods rotating about fixed points in opposite directions, we can follow these steps:
1. Understanding the Setup:
- We have two rods rotating about fixed points. Let's denote the fixed point for the first rod as O (at the origin, (0,0)) and the fixed point for the second rod as A (at (a,0)).
- The first rod rotates with an angular speed ω and the second rod rotates with an angular speed 2ω.
2. Position of the Rods:
- The angle of rotation for the first rod at time t is θ=ωt.
- The angle of rotation for the second rod at the same time t is 2θ=2ωt.
3. Coordinates of the Rods:
- The endpoint of the first rod can be represented in terms of θ:
P1=(L1cos(θ),L1sin(θ))
- The endpoint of the second rod can be represented in terms of 2θ:
P2=(a+L2cos(2θ),L2sin(2θ))
4. Finding the Intersection Point:
- Let the intersection point of the two rods be P(h,k).
- From the first rod, we have:
k=L1sin(θ)andh=L1cos(θ)
- From the second rod, we have:
k=L2sin(2θ)andh=a+L2cos(2θ)
5. Using Trigonometric Identities:
- We know that sin(2θ)=2sin(θ)cos(θ).
- Therefore, we can express k from the second rod as:
k=L2⋅2sin(θ)cos(θ)
6. Setting the Equations Equal:
- From the first rod, we have k=L1sin(θ).
- From the second rod, substituting for k:
L1sin(θ)=2L2sin(θ)cos(θ)
- Dividing both sides by sin(θ) (assuming sin(θ)≠0):
L1=2L2cos(θ)
7. Expressing h in Terms of k:
- From the first rod, we have h=L1cos(θ).
- Substituting L1:
h=2L2cos2(θ)
8. Relating h and k:
- We know k=L1sin(θ) and substituting L1:
k=2L2cos(θ)sin(θ)
- Using the identity sin(2θ)=2sin(θ)cos(θ):
k=L2sin(2θ)
9. Final Locus Equation:
- We can express h and k in terms of θ and eliminate θ to find the locus.
- After manipulation, we arrive at the equation:
3h2−2ah−k2=0
- This represents a hyperbola.
Conclusion:
The locus of the point of intersection of the two rods is a hyperbola given by the equation:
3x2−2ax−y2=0
- We have two rods rotating about fixed points. Let's denote the fixed point for the first rod as O (at the origin, (0,0)) and the fixed point for the second rod as A (at (a,0)).
- The first rod rotates with an angular speed ω and the second rod rotates with an angular speed 2ω.
- The angle of rotation for the first rod at time t is θ=ωt.
- The angle of rotation for the second rod at the same time t is 2θ=2ωt.
- The endpoint of the first rod can be represented in terms of θ:
P1=(L1cos(θ),L1sin(θ))
- The endpoint of the second rod can be represented in terms of 2θ:
P2=(a+L2cos(2θ),L2sin(2θ))
- Let the intersection point of the two rods be P(h,k).
- From the first rod, we have:
k=L1sin(θ)andh=L1cos(θ)
- From the second rod, we have:
k=L2sin(2θ)andh=a+L2cos(2θ)
- We know that sin(2θ)=2sin(θ)cos(θ).
- Therefore, we can express k from the second rod as:
k=L2⋅2sin(θ)cos(θ)
- From the first rod, we have k=L1sin(θ).
- From the second rod, substituting for k:
L1sin(θ)=2L2sin(θ)cos(θ)
- Dividing both sides by sin(θ) (assuming sin(θ)≠0):
L1=2L2cos(θ)
- From the first rod, we have h=L1cos(θ).
- Substituting L1:
h=2L2cos2(θ)
- We know k=L1sin(θ) and substituting L1:
k=2L2cos(θ)sin(θ)
- Using the identity sin(2θ)=2sin(θ)cos(θ):
k=L2sin(2θ)
- We can express h and k in terms of θ and eliminate θ to find the locus.
- After manipulation, we arrive at the equation:
3h2−2ah−k2=0
- This represents a hyperbola.
The locus of the point of intersection of the two rods is a hyperbola given by the equation:
3x2−2ax−y2=0
Topper's Solved these Questions
- HYPERBOLABOOK - CENGAGE ENGLISHCHAPTER - HYPERBOLAEXERCISE - SOLVED EXAMPLES
11 Videos
- HYPERBOLABOOK - CENGAGE ENGLISHCHAPTER - HYPERBOLAEXERCISE - CONCEPT APPLICATION EXERCISE 7.1
3 Videos
- HIGHT AND DISTANCE BOOK - CENGAGE ENGLISHCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives
3 Videos
- INDEFINITE INTEGRATIONBOOK - CENGAGE ENGLISHCHAPTER - INDEFINITE INTEGRATIONEXERCISE - Multiple Correct Answer Type
2 Videos
Similar Questions
Two straight lines rotate about two fixed points (-a, 0) and (a, 0) in antic clockwise direction. If they start from their position of coincidence such that one rotates at a rate double of the other, then locus of curve is
View SolutionThe locus of points inside a circle and equidistant from two fixed points on the circumference of the circle.
View Solution
Knowledge Check
Two people start jogging at the same point and time but in opposite directions. If the rate of on jogger is 2 mph faster than the other and after 3 hours they are 30 miles apart, what is the rate of the faster jogger?
A3B4C5D6
Two straight lines pass through the fixed points (±a,0) and have slopes whose products is p>0 Show that the locus of the points of intersection of the lines is a hyperbola.
View SolutionTwo straight lines pass through the fixed points (±a,0) and have slopes whose products is p>0 Show that the locus of the points of intersection of the lines is a hyperbola.
View SolutionA uniform rod AB hinged about a fixed point P is initially vertical. A rod is released from vertical position. When rod is in horizontal position:

The acceleration of the centre of mass of the rod is
View SolutionA uniform rod AB hinged about a fixed point P is initially vertical. A rod is released from vertical position. When rod is in horizontal position:
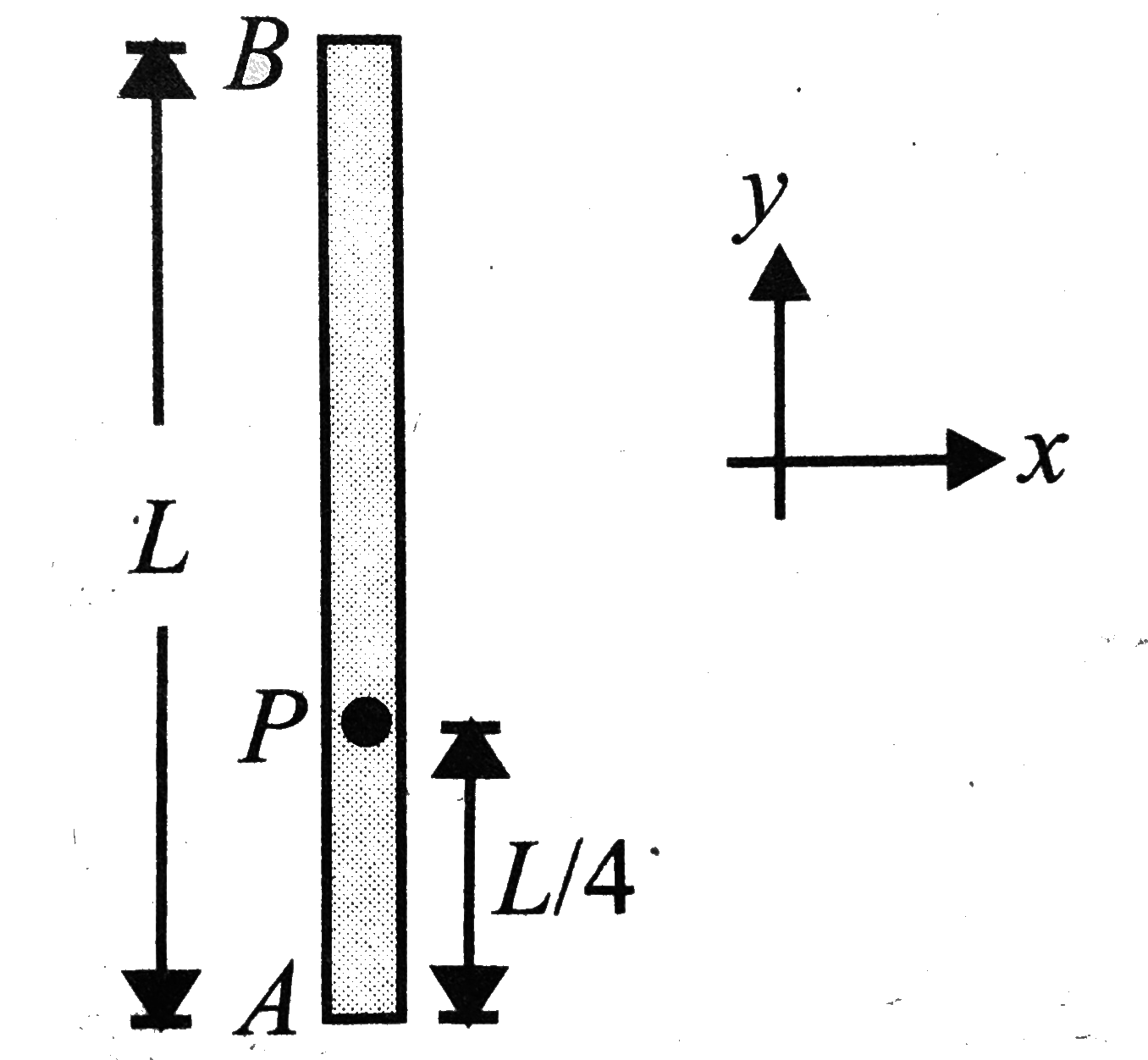
The acceleration of end B of the rod is
View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What is the rate of change of angular momentum of the rod ?

View SolutionA rod of mass m and length l is rotating about a fixed point in the ceiling with an angular velocity ω as shown in the figure. The rod maintains a constant angle θ with the vertical.
What will be the horizontal component of angular momentum of the rod about the point of suspension in terms of m, ω, l and θ.

View SolutionAn iron rod of length 2l is sliding on two mutually perpendicular lines . Find the locus of the midpoint of the rod.
View Solution
