Number of points with integral co-ordinates that lie inside a triangle whose co-ordinates are (0, 0), (0, 21) and (21,0).
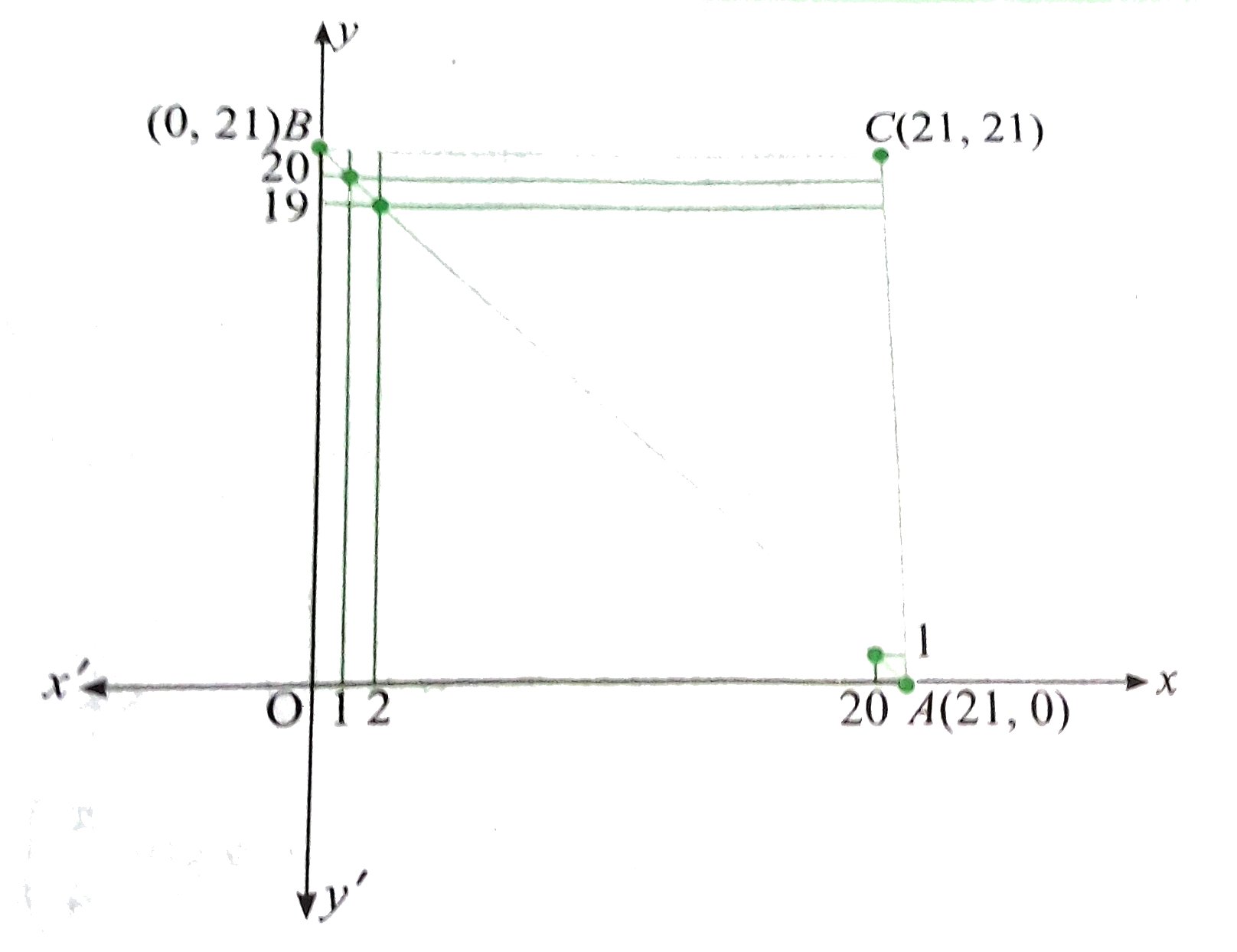
Total number of points within the square OACB=20×20=400 there are 20 points on the line AB which are (1,20),(2,19),......(20,1).
∴ Points within ΔOAB and ΔABC=400−20=380 by symmetry, points within ΔOAB=3802=190
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.21videos
COORDINATE SYSYEM
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.31videos
COORDINATE SYSYEM
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
- BOOK - CENGAGE ENGLISHCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.213videos
CROSS PRODUCTS
Similar Questions
Find the co-ordinates of the orthocentre of a triangle whose vertices are (3,−1), (−1,2) and (0,0).
View SolutionThe number of points, having both co-ordinates as integers, that lie in the interior of the triangle with vertices (0,0), (0,41) and (41,0) is
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionFind the Cartesian co-ordinates of point whose polar co-ordinates are (4,π3).
View SolutionNumber of integral points (integral points means both the co-ordinates should be integer) exactly in the interior of the triangle with vertices (0,0),(0,21)and(21,0) is
View SolutionNumber of integral points (integral points means both the co-ordinates should be integer) exactly in the interior of the triangle with vertices (0,0),(0,15)andOr(15,0) is
View SolutionFind the co-ordinates of the circumecentre of the triangle ABC, whose vertices A, B and C are (4, 6), (0,4) and (6,2) respectively.
View SolutionCalculate the co-ordinates of the centroid of the triangle ABC, if A = (7, -2), B = (0, 1) and C = (-1, 4).
View SolutionFind the co-ordinates of the points of tri section of the line joining the points (-3, 0) and (6, 6).
View SolutionFind the co-ordinates of the points fo trisection of the line segment joining the points (-2, 0) and (4, 0).
View Solution

