The straight line through a fixed point (2,3) intersects the coordinate axes at distinct point P and Q. If O is the origin and the rectangle OPRQ is completed then the locus of R is
3x+2y=6xy
3x+2y=6
2x+3y=xy
3x+2y=xy
The correct Answer is:D
To solve the problem step by step, we need to find the locus of point R, which is formed by the rectangle OPRQ, where O is the origin, P is on the x-axis, Q is on the y-axis, and the line passes through the fixed point (2, 3).
1. Understanding the Points:
- Let P be the point where the line intersects the x-axis, so P = (h, 0).
- Let Q be the point where the line intersects the y-axis, so Q = (0, k).
- The fixed point through which the line passes is (2, 3).
2. Equation of the Line:
- The line can be expressed in intercept form as:
xh+yk=1
3. Substituting the Fixed Point:
- Since the line passes through the point (2, 3), we substitute x = 2 and y = 3 into the line equation:
2h+3k=1
4. Clearing the Denominators:
- Multiply through by hk to eliminate the denominators:
2k+3h=hk
5. Rearranging the Equation:
- Rearranging gives:
hk−2k−3h=0
- This can be rewritten as:
hk−3h−2k=0
6. Expressing in Terms of x and y:
- Since we want the locus of point R, we replace h with x and k with y:
xy−3x−2y=0
7. Final Form:
- Rearranging gives us:
3x+2y=xy
Conclusion:
The locus of point R is given by the equation:
3x+2y=xy
- Let P be the point where the line intersects the x-axis, so P = (h, 0).
- Let Q be the point where the line intersects the y-axis, so Q = (0, k).
- The fixed point through which the line passes is (2, 3).
- The line can be expressed in intercept form as:
xh+yk=1
- Since the line passes through the point (2, 3), we substitute x = 2 and y = 3 into the line equation:
2h+3k=1
- Multiply through by hk to eliminate the denominators:
2k+3h=hk
- Rearranging gives:
hk−2k−3h=0
- This can be rewritten as:
hk−3h−2k=0
- Since we want the locus of point R, we replace h with x and k with y:
xy−3x−2y=0
- Rearranging gives us:
3x+2y=xy
The locus of point R is given by the equation:
3x+2y=xy
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Numerical value
12 Videos
- COORDINATE SYSTEMBOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE ENGLISHCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
A line is drawn through the point (1, 2) to meet the coordinate axes at P and Q such that it forms a triangle OPQ, where O is the origin. If the area of the triangle OPQ is least, then the slope of the line PQ is
View SolutionA straight line passes through the points A(-5, 2) and B(3,-6). It intersects the co-ordinate axes at points C and D . Find :
the equation of AB.
View SolutionIf a tangent to the circle x2+y2=1 intersects the coordinate axes at distinct points P and Q, then the locus of the mid-point of PQ is :
View SolutionA straight line passes through the points P(-1, 4) and Q(5,-2). It intersects the co-ordinate axes at points A and B. M is the midpoint of the segment AB. Find :

The equation of the line.
View SolutionA straight line passes through the points P(-1, 4) and Q(5,-2). It intersects the co-ordinate axes at points A and B. M is the midpoint of the segment AB. Find :
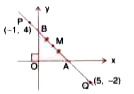
The co-ordinates of A and B.
View SolutionA straight line passes through the points P(-1, 4) and Q(5,-2). It intersects the co-ordinate axes at points A and B. M is the midpoint of the segment AB. Find :
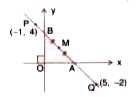
The co-ordinates of M.
View SolutionLet (h,k) be a fixed point, where h>0,k>0. A straight line passing through this point cuts the positive direction of the coordinate axes at the point PandQ . Find the minimum area of triangle OPQ,O being the origin.
View SolutionA variable line through the point (65,65) cuts the coordinates axes in the point AandB. If the point P divides AB internally in the ratio 2:1, show that the equation to the locus of P is :
View SolutionA straight line is drawn from a fixed point O meeting a fixed straight line in P. A point Q is taken on the line OP such that OP.OQ is constant. Show that the locus of Q is a circle.
View SolutionA variable line through the point (65,65) cuts the coordinate axes at the points A and B respectively. If the point P divides AB internally in the ratio 2:1, then the equation of the locus of P is
View Solution
