Find the length of altitude through of the triangle where
The correct Answer is:
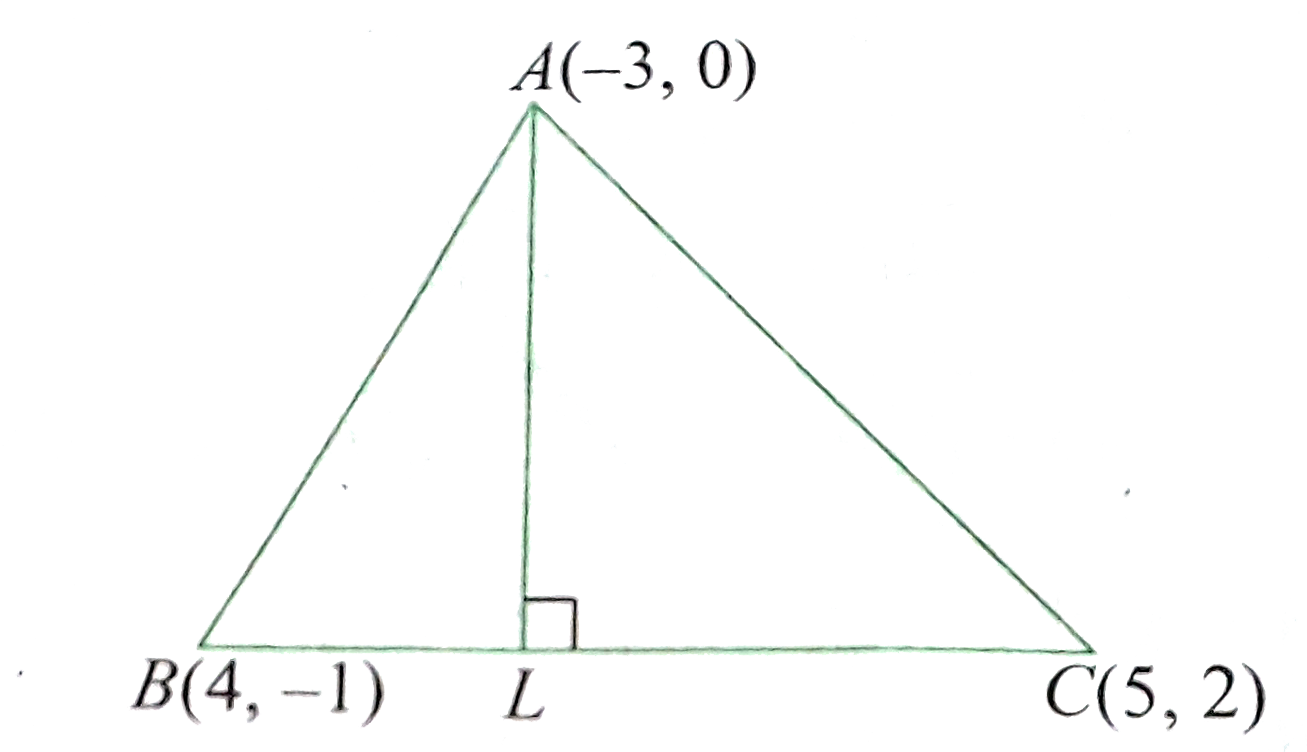
In the figure , AL is altitude .
Area of triangle
Also,
Now, area of triangle
.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Concept applications 1.310videos
COORDINATE SYSYEM
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Concept applications 1.48videos
COORDINATE SYSYEM
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Concept applications 1.16videos
COORDINATE SYSYEM
- BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
- BOOK - CENGAGE ENGLISHCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.213videos
CROSS PRODUCTS
Similar Questions
Find the equation of the altitudes of triangle ABC whose vertices are A(2,-2), B(1,1) and C(-1,0)
View SolutionFind the length of the medians of the triangle with vertices A(0,0,6), B(0,4,0) and C(6,0,0)
View SolutionFind the lengths of the medians of the triangle A(0,0,6),B(0,4,0)andC(6,0,0)
View SolutionFind the lengths of the sides of the triangle whose vertices are A(2,4,−1),(4,5,1),C(3,6,−3) and show that the triangle is right angled.
View SolutionThe equation of the altitude of the △ABC whose vertices are A(−4,2),B(6,5)andC(1,−4) can be
View SolutionFind the lengths of the medians of a triangle whose vertices are A(−1, 3), B(1, −1) and C(5, 1) .
View SolutionFind the orthocentre of ΔABC with vertices A(1,0),B(−2,1), and C(5,2)
View SolutionFind the orthocentre of ΔABC with vertices A(1,0),B(−2,1), and C(5,2)
View SolutionUsing integration, find the area of the triangle ABC whose vertices are A(−1,1),B(0,5) and C(3,2).
View SolutionCheck how the points A,B and C are situated where A(4,0),B(−1,−1),C(3,5) .
View Solution

