Question

Consider the traingle having vertices $O(0,0),A(2,0)$, and $B(1,\sqrt{3})$. Also $b\le \text{min}\{a_1,a_2,a_3....a_n\}$ means $b\le a_1$ when $a_1$ is least, $b\le a_2$ when $a_2$ is least, and so on. Form this, we can say $b\le a_1,b\le a_2,.....b\le a_n$.
Let R be the region consisting of all those points P inside $\Delta OAB$ which satisfy $d(P,OA)\le \text{min}[d(P,OB),d(P,AB)]$, where d denotes the distance from the point to the corresponding line. then the area of the region R is

Options

A. `sqrt(3)`sq,units
B. `1//sqrt(3)` sq.units
C. `sqrt(3)//2`sq,units
D. none of these

Answer

B

Explanation

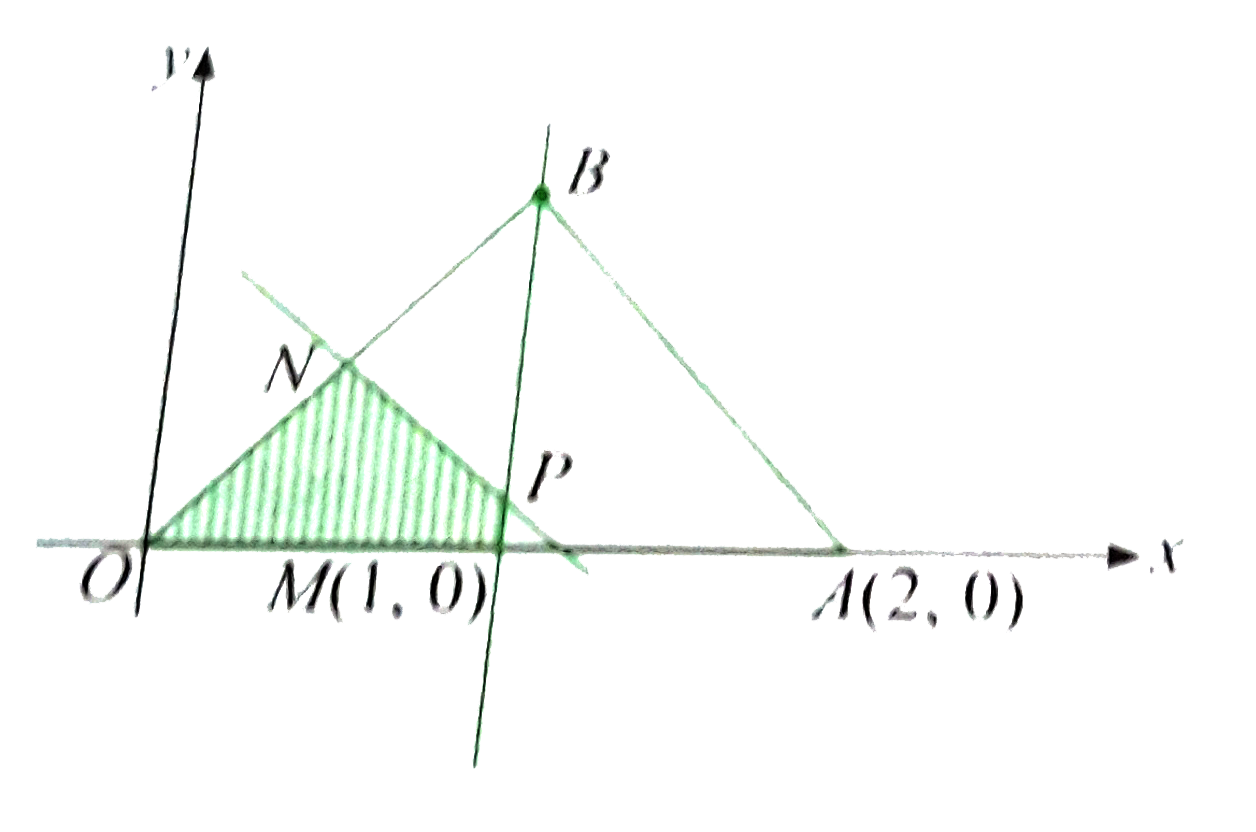
`OP le "min"[BP,AP]`
`OP le AP(whenAPlt BP)`
Let `OP=BP`. The P lies on the perpendicular bisector of OB, For `OP=AP,P` lies on the perpendiuclar bisector of OA. Then, for the required condition, P lies in the region as shown in the diagram. the area of region `OMPN` is
`(1)/(2)xx|{:(0,,0,,),(1,,0,,),(1,,1//sqrt3,,),(1/2,,sqrt(3)//2,,),(0,,0,,):}|=(1)/(2)[(1)/(sqrt3)+(sqrt3)/(2)-(1)/(2sqrt3)]`
`=(1)/(2)[sqrt(3)/(2)+(1)/(sqrt3)]=(1)/(sqrt3)`