Line AB passes through point (2,3) and intersects the positive x and y-axes at A(a,0) and B(0,b) respectively. If the area of ΔAOB is 11. then the value of 4b2+9a2 is
The correct Answer is:220
Area of ΔAOB,ab2=11
∴ab=22,
But points A(a,0),B(0,b) and P(2,3) are collinear. ⇒ Slope of AB = Slope of AP
⇒ba=3−02−a
⇒−2b+ab=3a
Squareing 9a2+ab2+12ab=484
⇒9a2+4b2=220
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - JEE Main
6 Videos
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Matrix match type
4 Videos
- COORDINATE SYSTEMBOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE ENGLISHCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
A straight line through the point (2,2) intersects the lines √3x+y=0 and √3x−y=0 at the point A and B, respectively. Then find the equation of the line AB so that triangle OAB is equilateral.
View SolutionA straight line through the point (2,2) intersects the lines √3x+y=0 and √3x−y=0 at the point A and B, respectively. Then find the equation of the line AB so that triangle OAB is equilateral.
View SolutionA straight line passes through the points A(-5, 2) and B(3,-6). It intersects the co-ordinate axes at points C and D . Find :
the equation of AB.
View SolutionA straight line through the point A (−2,−3) cuts the line x+3y=9 and x+y+1=0 at B and C respectively. If AB.AC=20 then equation of the possible line is
View SolutionFind the equations to the straight lines which pass through the point (−2,3) and cut the axes at A(a,0)andB(0,b) so that a+b=2
View SolutionThe graph of a line in the xy-plane passes through the point (1, 4) and crosses the x-axis at the point (2, 0). The line crosses the y-axis at the point (0, b). What is the value of b ?
View SolutionA straight line passes through the points P(-1, 4) and Q(5,-2). It intersects the co-ordinate axes at points A and B. M is the midpoint of the segment AB. Find :
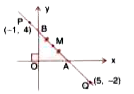
The co-ordinates of A and B.
View SolutionSuppose a parabola y=x2−ax−1 intersects the coordinate axes at three points A,B and C, respectively. The circumcircle of ΔABC intersects the y-axis again at the point D(0,t). Then the value of t is
View SolutionIf a circle passes through the points of intersection of the lines 2x−y+1=0 and x+λy−3=0 with the axes of reference then the value of λ is :
View SolutionA circle of radius 1 unit touches the positive x-axis and the positive y-axis at A and B , respectively. A variable line passing through the origin intersects the circle at two points D and E . If the area of triangle DEB is maximum when the slope of the line is m, then find the value of m−2
View Solution