Prove that the coefficient of xn in the expansion of 1(1−x)(1−2x)(1−3x)is12(3n+2−2n+3+1).
We have,
1(1−x)(1−2x)(1−3x)
=12(1−x)−41−2x+92(1−3x) [By resolving into partial fractions]
=12(1−x)−1−4(1−2x)−1+92(1−3x)−1
=12(1+x+x2+….+xn+….)
−4(1+2x+(2x)2+….+(2x)n+....)
+92(1+(3x)+(3x)2+....+(3x)n+....)
∴ Coefficient of xn=12[1−8×2n+9×3n]
=12[1−2n+3+3n+2]
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Example10videos
BINOMIAL THEOREM
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Concept Application Exercise 8.117videos
BINOMIAL THEOREM
- BOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Comprehension Type2videos
AREA
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE7videos
CIRCLE
Similar Questions
The coefficient of xn in the expansion of 1(1−x)(3−x), is
View SolutionThe coefficient of xnin the expansion of
(1+x1−x)2, isView SolutionFind the coefficient of xn in the expansion of (1−9x+20x2)−1.
View SolutionThe coefficient of xn in the expansion of (1+x)2(1−x)3, is
View SolutionProve that the coefficient of xr in the expansion of (1−2x)1/2is(2r)!/[2r(r!)2].
View SolutionThe coefficient of xn in the expansion of
loge(1+3x+2x2) isView SolutionProve that the coefficient of x3 in the expansion of (1+x+2x2)(2x2−13x)9 is −22427.
View SolutionIf 'n' is a positive integer then prove that the coefficient foxm in the expansion of (x2+1x)2n is :
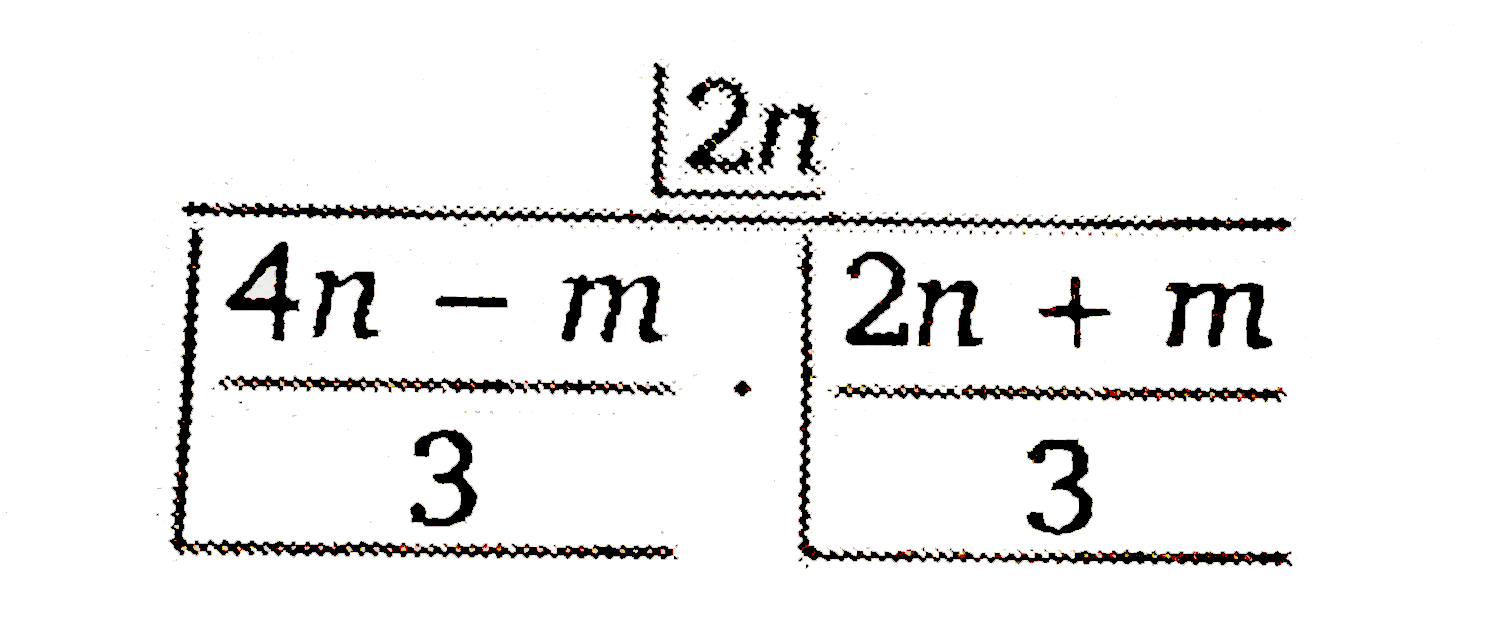View SolutionIf 'n' is a positive integer then prove that the coefficient foxm in the expansion of (x2+1x)2n is :
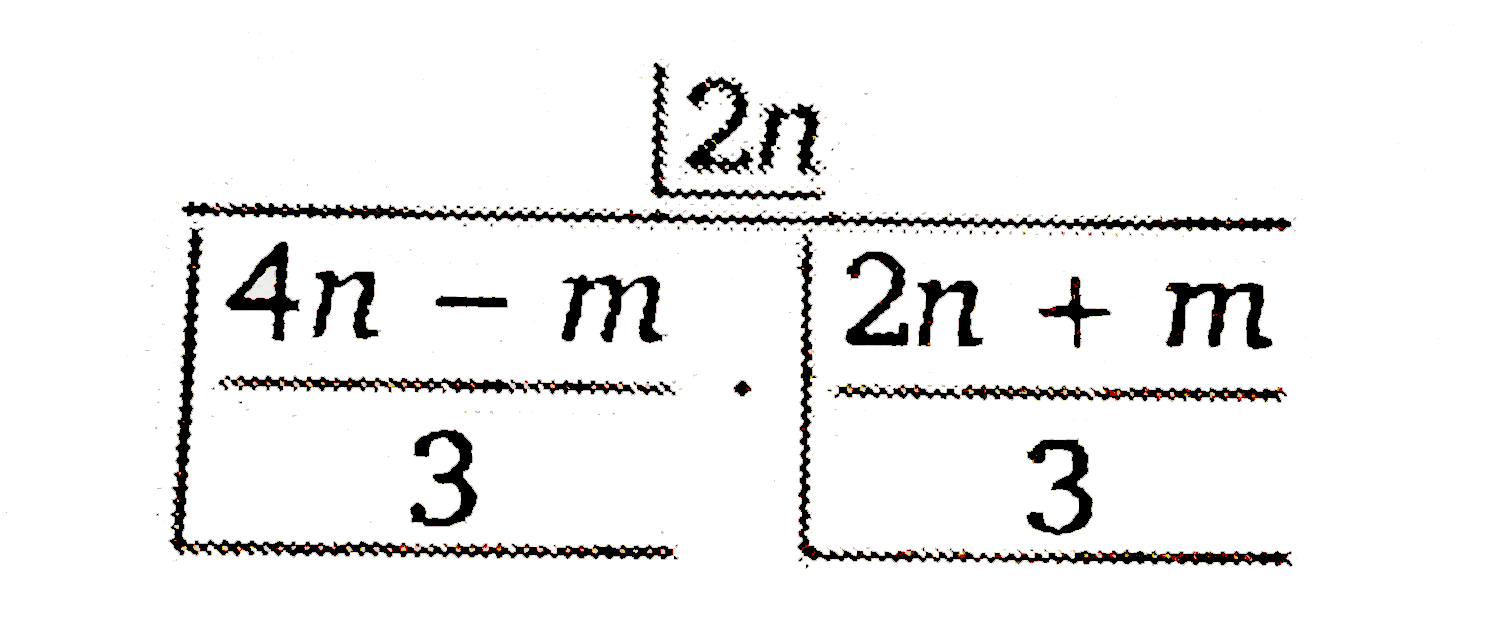View SolutionThe sum of the coefficients in the expansion of (1−x+x2−x3)n ,is
View Solution