Consider one sides AB of a square ABCD in order on line y=2x−17, and other two vertices C, D on y=x2
The maximum possible area of square ABCD is
1180
1250
1280
none
The correct Answer is:C
To find the maximum possible area of square ABCD, where one side AB lies on the line y=2x−17 and the other two vertices C and D lie on the parabola y=x2, we can follow these steps:
Step 1: Define the side length of the square
Let the side length of the square be a. The area of the square will then be A=a2.
Step 2: Determine the equation of line CD
Since line CD is parallel to line AB, it will have the same slope. The equation of line CD can be expressed as:
y=2x+b
where b is a constant.
Step 3: Find the coordinates of points B and C
Let the coordinates of point B be (x2,y2) and point C be (x1,y1). Since points B and C lie on the line y=2x−17, we have:
y2=2x2−17
y1=2x1−17
Step 4: Find the slope of line CD
The slope of line CD is given by:
mCD=y2−y1x2−x1
Substituting the values of y2 and y1:
mCD=(2x2−17)−(2x1−17)x2−x1=2(x2−x1)x2−x1=2
This confirms that line CD has a slope of 2.
Step 5: Use the distance formula
The length of line segment CD must equal the side length a of the square. Using the distance formula:
CD=√(x2−x1)2+(y2−y1)2
Substituting for y2 and y1:
CD=√(x2−x1)2+((2x2−17)−(2x1−17))2
This simplifies to:
CD=√(x2−x1)2+(2(x2−x1))2=√(x2−x1)2+4(x2−x1)2=√5(x2−x1)2=√5|x2−x1|
Setting this equal to a:
a=√5|x2−x1|
Step 6: Relation between points C and D on the parabola
Since points C and D lie on the parabola y=x2, we have:
y1=x21andy2=x22
Thus, we can express y2−y1 as:
y2−y1=x22−x21=(x2−x1)(x2+x1)
Step 7: Substitute into the distance formula
From the previous steps, we know:
a=√5|x2−x1|
Substituting y2−y1 into the distance formula gives:
a=√5|x2−x1|=|(x2−x1)(x2+x1)|
This leads to:
√5=|x2+x1|
Step 8: Use the quadratic equation
The points x1 and x2 are the roots of the quadratic equation formed by equating the line and the parabola:
x2−2x−b=0
Using Vieta's formulas, we have:
x1+x2=2andx1x2=−b
Step 9: Find the maximum area
We have two relations:
1. a2=20(1+b)
2. a2=5(b+17)
Setting these equal gives:
20(1+b)=5(b+17)
Solving this equation will yield values for b.
Step 10: Solve for b
20+20b=5b+85
15b=65⟹b=6515=133
Step 11: Calculate a2
Substituting b back into either equation for a2:
a2=20(1+133)=20⋅163=3203
Step 12: Find the maximum area
The maximum area of square ABCD is:
A=a2=1280
Thus, the maximum possible area of square ABCD is 1280.
---
Let the side length of the square be a. The area of the square will then be A=a2.
Since line CD is parallel to line AB, it will have the same slope. The equation of line CD can be expressed as:
y=2x+b
where b is a constant.
Let the coordinates of point B be (x2,y2) and point C be (x1,y1). Since points B and C lie on the line y=2x−17, we have:
y2=2x2−17
y1=2x1−17
The slope of line CD is given by:
mCD=y2−y1x2−x1
Substituting the values of y2 and y1:
mCD=(2x2−17)−(2x1−17)x2−x1=2(x2−x1)x2−x1=2
This confirms that line CD has a slope of 2.
The length of line segment CD must equal the side length a of the square. Using the distance formula:
CD=√(x2−x1)2+(y2−y1)2
Substituting for y2 and y1:
CD=√(x2−x1)2+((2x2−17)−(2x1−17))2
This simplifies to:
CD=√(x2−x1)2+(2(x2−x1))2=√(x2−x1)2+4(x2−x1)2=√5(x2−x1)2=√5|x2−x1|
Setting this equal to a:
a=√5|x2−x1|
Since points C and D lie on the parabola y=x2, we have:
y1=x21andy2=x22
Thus, we can express y2−y1 as:
y2−y1=x22−x21=(x2−x1)(x2+x1)
From the previous steps, we know:
a=√5|x2−x1|
Substituting y2−y1 into the distance formula gives:
a=√5|x2−x1|=|(x2−x1)(x2+x1)|
This leads to:
√5=|x2+x1|
The points x1 and x2 are the roots of the quadratic equation formed by equating the line and the parabola:
x2−2x−b=0
Using Vieta's formulas, we have:
x1+x2=2andx1x2=−b
We have two relations:
1. a2=20(1+b)
2. a2=5(b+17)
20(1+b)=5(b+17)
Solving this equation will yield values for b.
20+20b=5b+85
15b=65⟹b=6515=133
Substituting b back into either equation for a2:
a2=20(1+133)=20⋅163=3203
The maximum area of square ABCD is:
A=a2=1280
Topper's Solved these Questions
- PARABOLABOOK - CENGAGE ENGLISHCHAPTER - PARABOLAEXERCISE - MATRIX MATCH TYPE
5 Videos
- PARABOLABOOK - CENGAGE ENGLISHCHAPTER - PARABOLAEXERCISE - NUMERICAL VALUE TYPE
32 Videos
- PARABOLABOOK - CENGAGE ENGLISHCHAPTER - PARABOLAEXERCISE - EXERCISE (MULTIPLE CORRECT ANSWER TYPE )
26 Videos
- PAIR OF STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - PAIR OF STRAIGHT LINESEXERCISE - Numberical Value Type
5 Videos
- PERMUTATION AND COMBINATIONBOOK - CENGAGE ENGLISHCHAPTER - PERMUTATION AND COMBINATIONEXERCISE - Comprehension
8 Videos
Similar Questions
Consider one sides AB of a square ABCD in order on line y=2x−17, and other two vertices C, D on y=x2
The minimum intercept of line CD on the y-axis is
View SolutionOne side of square ABCD is on the line y=2x−17 and other two vertices are on parabola y=x2, if the minimum area of square is A then find A16.
View Solution
Knowledge Check
In the figure, ABCD is a square, and BC is tangent to the circle with radius 3. If PC = 2, then what is the area of square ABCD?
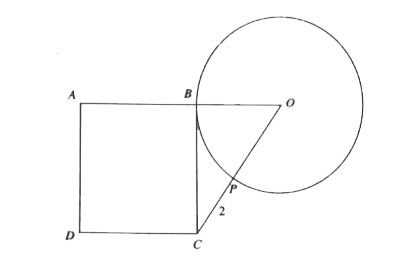 A9B13C16D18
A9B13C16D18If a vertex of a square is at the point (1,−1) and one of its sides lie along the line 3x−4y−17=0, then the area of the square is
A4 sq. unitsB3 sq. unitsC12 sq. unitsD2 sq. units
Two sides of a square lie on the lines x+y=1andx+y+2=0. What is its area?
View SolutionTwo sides of a square lie on the lines x+y=1andx+y+2=0. What is its area?
View SolutionTwo sides of a square lie on the lines x+y=1andx+y+2=0. What is its area?
View SolutionThe largest area of a rectangle which has one side on the x-axis and the two vertices on the curve y=e−x2 is
View SolutionLet ABCD be a square of side length 2 units. C2 is the circle through vertices A, B, C, D and C1 is the circle touching all the sides of the square ABCD. L is a line through A. . If P is a point on C1 and Q in another point on C2, then (PA^2+ PB^2+ PC^2+PD^2)/ (QA^2+ QB^2+ QC^2+ QD^2) is equal to (A) 0.75 (B) 1.25 (C) 1 (D) 0.5
View SolutionThe side AB of a square ABCD is parallel to the x-axis. Find the slopes of all its sides.

Also, find :
the slope of the diagonal AC.
View Solution
