In a quadrillateral ABCD, it is given that AB ||CD and the diagonals AC and BD are perpendiclar to each other . Show that AD.BC≥AB.CD.
Let AC and BD intersect at O (origin)
According to the question →a.→b=0
Also AB||CD
(μ→a−λ→b)∣∣(→a−→b)
⇒μ=λ
LetAD.BC≥AB.CD
⇒∣∣λ→b−→a∣∣∣∣μ→a−→b∣∣|≥|(→b−→a)∣∣∣(λ→b−μ→a)∣∣
or(λ2b2+a2)(μ2a2+b2)≥(b2+a2)(λ2b2+μ2a2)
orλ2μ2a2b2+a2b2≥λ2a2b2+μ2b2a2
or(λ92)−1)(μ2−1)≥0
or(λ2−1)2≥0 which is true.
Hence, AD. BC ≥ AB. CD

Topper's Solved these Questions
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercises MCQ
134 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Reasoning type
8 Videos
- DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS BOOK - CENGAGE ENGLISHCHAPTER - DIFFERENT PRODUCTS OF VECTORS AND THEIR GEOMETRICAL APPLICATIONS EXERCISE - Exercise 2.3
18 Videos
- DETERMINANTSBOOK - CENGAGE ENGLISHCHAPTER - DETERMINANTSEXERCISE - All Questions
264 Videos
- DIFFERENTIAL EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Matrix Match Type
5 Videos
Similar Questions
In a quadrilateral ABCD, it is given that AB∣∣CD and the diagonals ACandBD are perpendicular to each other. Show that AD.BC≥AB.CD.
View SolutionABCD is a trapezium such that AB||CD. Its diagonals AC and BC intersect each other at O. Prove that AOOC=BOOD
View SolutionIn quadrilateral ABCD, AB=DC and AD=BC. Prove that the sides AB and DC are parallel to each other.
View SolutionIn a trapezium ABCD, side AB is parallel to side DC, and the diagonals AC and BD intersect each other at point P. Prove that :
ΔAPB is similar to ΔCPD.
View SolutionIn a quadrilateral ABCD, AB = CD and ∠B=∠C. Prove that
AC=AB
View SolutionIn a quadrilateral ABCD, AB= AD and CB= CD. Prove that:
AC bisects angle BAD
View SolutionIn the figure AB = BC and AD is perpendicular to CD. Prove that :
AC2=2.BC.DC
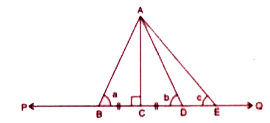
View SolutionIn the given figure, AC is perpendicular to line PQ and BC = CD. Show that AE is greater than AB.
View SolutionIf ABCD is a quadrilateral such that AB = AD and CB = CD , then prove that AC is the perpendicular bisector of BD.
View SolutionIn a quadrilateral ABCD, AB = AD and CB = CD. Prove that :
(i) AC bisects angle BAD
(ii) AC is perpendicular bisector of BD.
View Solution
