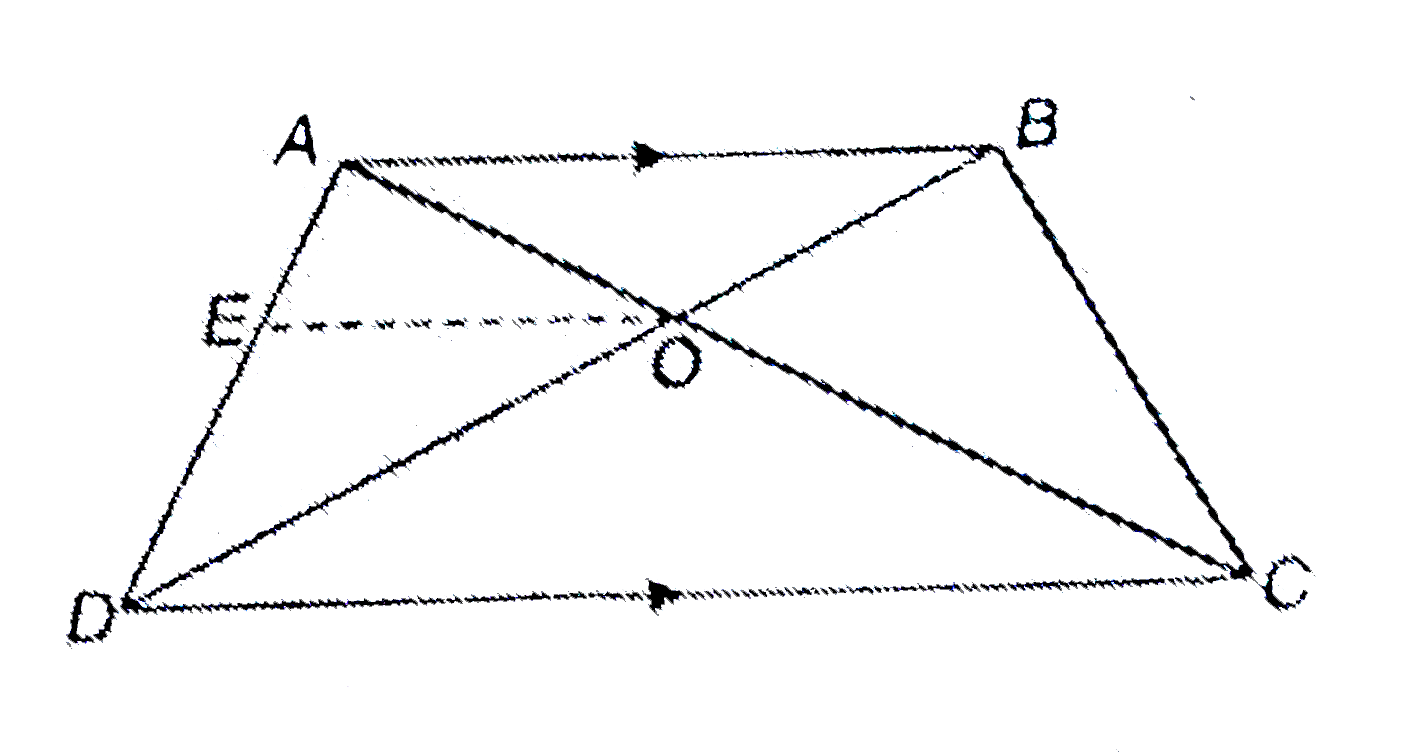
ABCD is a trapezium such that AB||CD. Its diagonals AC and BC intersect each other at O. Prove that
Draw EO||AB||CD
Now.in , since EO||DC
( by B.P theorem) ….(1)
In , since EO||AB
( by B.P theorem) …(2)
From (1) and (2) , we have
Topper's Solved these Questions
- TRIANGLES Book:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLES Exercise:Problems From NCERT/ Exemplar
Explore 14 Videos
- TRIANGLES Book:NAGEEN PRAKASHAN ENGLISHChapter:TRIANGLES Exercise:Exercise 6a
Explore 24 Videos
- STATISTICS Book:NAGEEN PRAKASHAN ENGLISHChapter:STATISTICS Exercise:Revision Exercise Long Answer Questions
Explore 4 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBook:NAGEEN PRAKASHAN ENGLISHChapter:VOLUME AND SURFACE AREA OF SOLIDSExercise:Revisions Exercise Long Answer Questions
Explore 5 Videos
Similar Questions
ABCD is a trapezium in which AB||DC and its diagonals intersect each other at the point O. Show that AOBO=CODO.
View SolutionDiagonals of rhombus ABCD intersect each other at point O. Prove that :
OA2+OC2=2AD2−BD22
View SolutionIn a trapezium ABCD, side AB is parallel to side DC, and the diagonals AC and BD intersect each other at point P. Prove that :
PA×PD=PB×PC.
View SolutionIn the adjoining figure, ABCD is a quadrilateral. Its diagonals AC and BD intersect at point 'O'. Prove that :
(a) AB+BC+CD+DA<2(AC+BD)
(b) AB+BC+CD+DA>(AC+BD)

View SolutionIn a trapezium ABCD, side AB is parallel to side DC, and the diagonals AC and BD intersect each other at point P. Prove that :
ΔAPB is similar to ΔCPD.
View SolutionDiagonals AC and BD of a trapezium ABCD with AB∣∣DC intersect each other at O . Prove that ar (AOD)= ar (BOC) .
View SolutionIn a quadrilateral ABCD, it is given that AB∣∣CD and the diagonals ACandBD are perpendicular to each other. Show that AD.BC≥AB.CD.
View SolutionIn the adjoining figure, ABCD is a quadrilateral in which AD∣∣BC. AC and BD intersect each other at point 'O'. Prove that:
area of ΔCOD= area of ΔABO
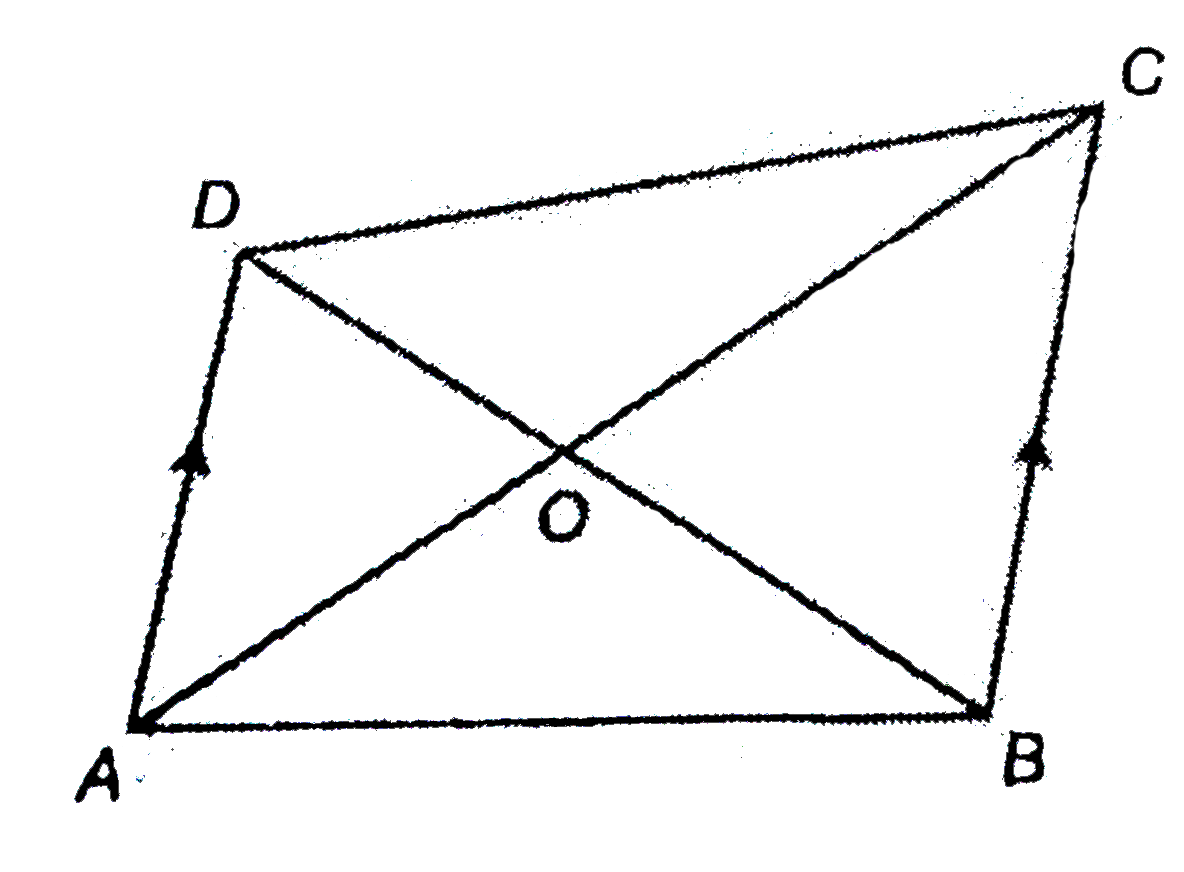
View SolutionDiagonals AC and BD of a trapezium ABCD with AB∣∣CD intersect each other at O. Prove that ar (△AOD)=ar(△BOC).
View SolutionABCD is a trapezium with AB∣∣DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar (ADX) = ar (ACY).
View Solution