Question

Three circles touch each other externally. The tangents at their point of contact meet at a point whose distance from a point of contact is 4. Then, the ratio of their product of radii to the sum of the radii is

Explanation

To solve the problem, we need to find the ratio of the product of the radii of three circles that touch each other externally to the sum of their radii. Let's denote the radii of the circles as $$r_1,r_2,$$ and $$r_3$$.

1. Understanding the Setup:
- We have three circles that touch each other externally. The tangents at the points of contact meet at a point, and the distance from this point to the point of contact is given as 4.

2. Using Triangle Properties:
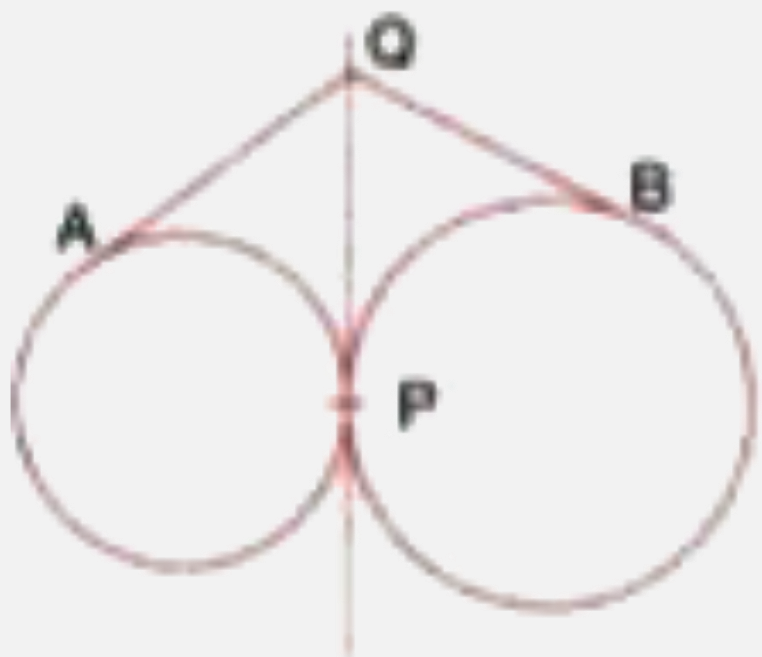
- Consider one of the circles and the triangle formed by the radius to the point of contact and the tangents. Let’s denote the point of contact as \( A \), the center of the circle as \( O \), and the point where the tangents meet as \( P \).
- The distance \( PA = 4 \).

3. Using Tangent Properties:
- For the triangle \( OAP \):
- The angle at \( P \) can be denoted as \( \alpha \) for the first circle, \( \beta \) for the second circle, and \( \gamma \) for the third circle.
- The angles at \( P \) satisfy the equation \( 2\alpha + 2\beta + 2\gamma = 360^\circ \) or \( 2\pi \) radians, which simplifies to \( \alpha + \beta + \gamma = \pi \).

4. Finding Tangent Values:
- By the definition of tangent in right triangles:
- \( \tan(\alpha) = \frac{r_1}{4} \)
- \( \tan(\beta) = \frac{r_2}{4} \)
- \( \tan(\gamma) = \frac{r_3}{4} \)

5. Using the Tangent Addition Formula:
- From the angle sum property, we have:
\( \tan(\alpha + \beta) = \tan(\pi - \gamma) = -\tan(\gamma) \)
- Using the tangent addition formula:
\( \tan(\alpha + \beta) = \frac{\tan(\alpha) + \tan(\beta)}{1 - \tan(\alpha)\tan(\beta)} \)
- This leads to the equation:
\( \frac{\frac{r_1}{4} + \frac{r_2}{4}}{1 - \frac{r_1 r_2}{16}} = -\frac{r_3}{4} \)

6. Setting Up the Equation:
- Rearranging gives:
\( \frac{r_1 + r_2}{4} = -\frac{r_3}{4}(1 - \frac{r_1 r_2}{16}) \)
- This simplifies to:
\( r_1 + r_2 + r_3 = \frac{r_1 r_2 r_3}{16} \)

7. Finding the Ratio:
- We need to find the ratio of the product of the radii to the sum of the radii:
\( \frac{r_1 r_2 r_3}{r_1 + r_2 + r_3} \)
- Substituting from our previous result:
\( \frac{r_1 r_2 r_3}{\frac{r_1 r_2 r_3}{16}} = 16 \)

8. Final Result:
- Therefore, the ratio of the product of the radii to the sum of the radii is:
\( \text{Ratio} = 16 : 1 \)