If the median AD of triangle ABC makes an angle π4 with the side BC, then find the value of |cotB−cotC|.

By m−n theorem,
(BD+DC)cot.π4=DCcotB−BDcotC
⇒|cotB−cotC|=2
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.112videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.28videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Numerical Value Type)3videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )1videos
PROGRESSION AND SERIES
- BOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Archives(Matrix Match Type)1videos
RELATIONS AND FUNCTIONS
Similar Questions
If the median AD of a triangle ABC makes an angle θ with side, AB, then sin(A−θ) is equal to
View SolutionIf median AD of a triangle ABC makes angle π6 with side BC, then the valur of (cotB−cotC)2 is equal to
View SolutionIf the bisector of angle A of the triangle ABC makes an angle θ with BC, then sinθ=
View SolutionThe sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and the median PM of triangle PQR respectively. Prove that the triangles ABC and PQR are congruent.
View SolutionIn ABC, if cotA+cotB+cotC=0 then find the value of cosAcosBcosC
View SolutionIn the following figures, the sides AB and BC and the median AD of triangle ABC are respectively equal to the sides PQ and QR and median PS of the triangle PQR. Prove that ΔABCandΔPQR are congruent.
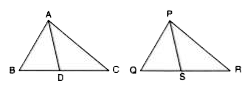 View Solution
View SolutionIn a triangle ABC,vertex angles A,B,C and side BC are given .The area of △ABC is
View SolutionLet H be the orthocentre of triangle ABC. Then angle subtended by side BC at the centre of incircle of ΔCHB is
View SolutionAD is a median of triangle ABC. Prove that : AB+AC>2AD
View SolutionAD is a median of triangle ABC. Prove that : AB+BC+AC>2AD
View Solution

