AD is a median of triangle ABC. Prove that :
To prove that AB+AC>2AD where AD is the median of triangle ABC, we can follow these steps:
1. Draw Triangle ABC:
- Start by drawing triangle ABC with D as the midpoint of side BC. This means BD=DC.
2. Construct Point E:
- Extend line segment AD to a point E such that AD=DE. This means E is located such that AE=AD+DE=2AD.
3. Triangles to Consider:
- Now, consider triangles ABD and CDE.
4. Identify Angles:
- Note that ∠ADB and ∠CDE are vertically opposite angles, so they are equal. Let's denote them as ∠1 and ∠2.
5. Use Midpoint Property:
- Since D is the midpoint of BC, we have BD=DC.
6. Apply Construction:
- By construction, AD=DE.
7. Congruent Triangles:
- Now, we can show that triangles ABD and CDE are congruent by the Side-Angle-Side (SAS) criterion:
- BD=DC (since D is the midpoint),
- AD=DE (by construction),
- ∠ADB=∠CDE (vertically opposite angles).
- Therefore, △ABD≅△CDE.
8. Corresponding Parts:
- By the property of congruent triangles (CPCT), we have AB=EC.
9. Apply Triangle Inequality:
- Now, consider triangle AEC. By the triangle inequality, we know that the sum of any two sides of a triangle must be greater than the third side:
- Thus, AC+EC>AE.
10. Substitute EC:
- We already established that EC=AB. Substituting this into the inequality gives:
AC+AB>AE
11. Express AE:
- From our construction, AE=AD+DE=AD+AD=2AD.
12. Final Inequality:
- Therefore, we can write:
AB+AC>2AD
Conclusion:
Thus, we have proved that AB+AC>2AD.
- Start by drawing triangle ABC with D as the midpoint of side BC. This means BD=DC.
- Extend line segment AD to a point E such that AD=DE. This means E is located such that AE=AD+DE=2AD.
- Now, consider triangles ABD and CDE.
- Note that ∠ADB and ∠CDE are vertically opposite angles, so they are equal. Let's denote them as ∠1 and ∠2.
- Since D is the midpoint of BC, we have BD=DC.
- By construction, AD=DE.
- Now, we can show that triangles ABD and CDE are congruent by the Side-Angle-Side (SAS) criterion:
- BD=DC (since D is the midpoint),
- AD=DE (by construction),
- ∠ADB=∠CDE (vertically opposite angles).
- Therefore, △ABD≅△CDE.
- By the property of congruent triangles (CPCT), we have AB=EC.
- Now, consider triangle AEC. By the triangle inequality, we know that the sum of any two sides of a triangle must be greater than the third side:
- Thus, AC+EC>AE.
- We already established that EC=AB. Substituting this into the inequality gives:
AC+AB>AE
- From our construction, AE=AD+DE=AD+AD=2AD.
- Therefore, we can write:
AB+AC>2AD
Thus, we have proved that AB+AC>2AD.
Topper's Solved these Questions
Similar Questions
AD is a median of triangle ABC. Prove that : AB+BC+AC>2AD
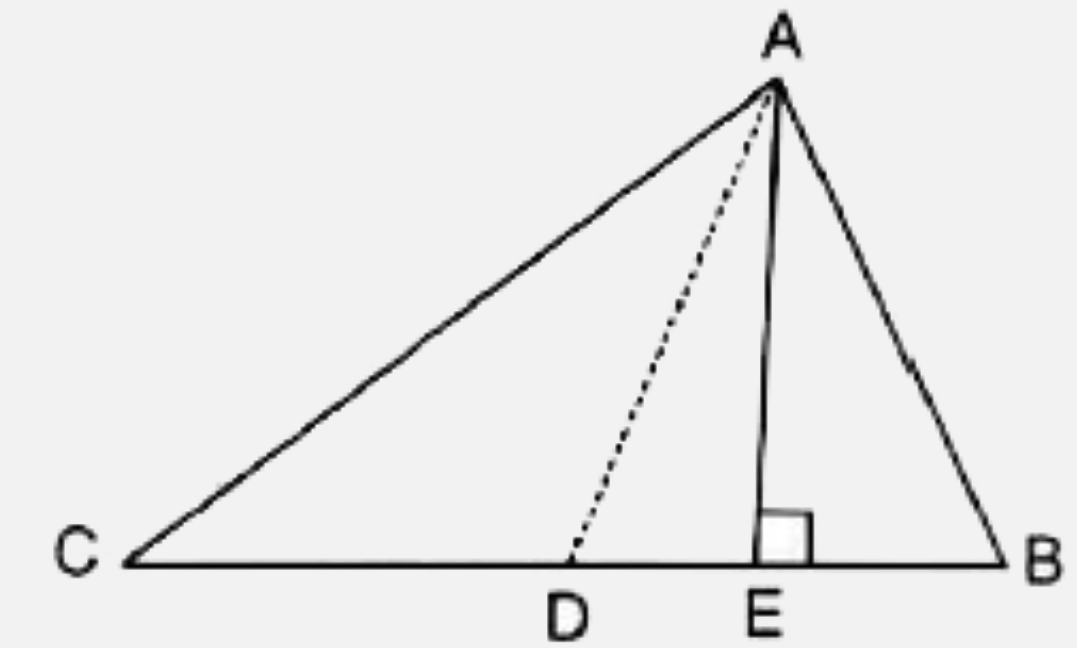
View SolutionThe following figures shows a triangle ABC in which AD is median and AE⊥BC.
Prove that : 2AB2+2AC2=4AD2+BC2
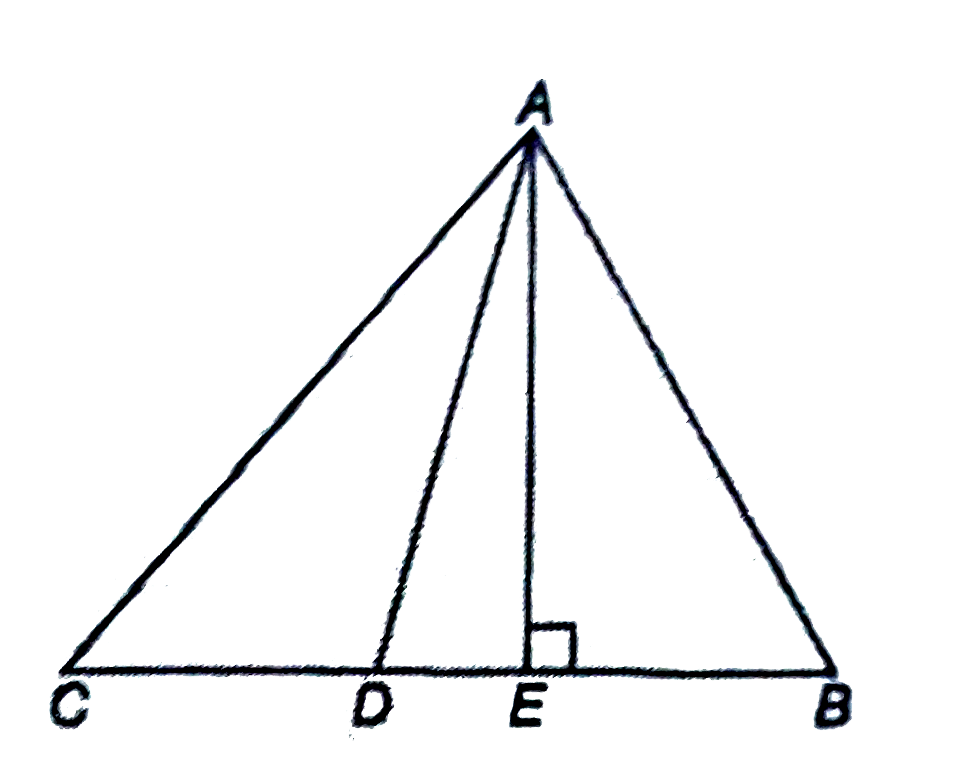
View SolutionThe following figure shows a triangle ABC in which AD is a median and AE⊥BC. Prove that 2AB2+2AC2=4AD2+BC2 .
View SolutionIn the following figures, the sides AB and BC and the median AD of triangle ABC are respectively equal to the sides PQ and QR and median PS of the triangle PQR. Prove that ΔABCandΔPQR are congruent.

View SolutionIf D any point on the BC of an isosceles triangle ABC then prove that AB>AD and AC>AD.

View SolutionIn the figure, AD is perpendicular to BC, prove that AB+AC>2AD.

View SolutionIn triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View SolutionIn triangle ABC, AB>AC and D is a point in side BC. Show that : AB>AD.
View SolutionThe given figure shows an equilateral triangles ABC and D is point in AC.
Prove that :
(i) AD<BD
(ii)BC>BD
View SolutionAD is a median of the ΔABC.Is it trure AB+BC+CA>2AD? Give reason for your answer
View Solution