Let the lengths of the altitudes drawn from the vertices of ΔABC to the opposite sides are 2, 2 and 3. If the area of ΔABC is Δ, then find the area of triangle
The correct Answer is:92√2 sq. unit
To solve the problem, we need to find the area of triangle ABC given the lengths of the altitudes from its vertices to the opposite sides. The altitudes are given as follows:
- ha=2 (altitude from vertex A to side BC)
- hb=2 (altitude from vertex B to side AC)
- hc=3 (altitude from vertex C to side AB)
Let the area of triangle ABC be denoted as Δ.
Step 1: Express the area in terms of the sides and altitudes
The area Δ of triangle ABC can be expressed using the formula for the area in terms of the base and height:
1. Using BC as the base:
Δ=12×a×ha=12×a×2=a
(Equation 1)
2. Using AC as the base:
Δ=12×b×hb=12×b×2=b
(Equation 2)
3. Using AB as the base:
Δ=12×c×hc=12×c×3=32c
(Equation 3)
Step 2: Relate the sides to the area
From the equations derived, we can express the sides a,b, and c in terms of the area Δ:
- From Equation 1: a=Δ
- From Equation 2: b=Δ
- From Equation 3: c=23Δ
Step 3: Calculate the semi-perimeter
The semi-perimeter s of triangle ABC is given by:
s=a+b+c2=Δ+Δ+23Δ2=2Δ+23Δ2=63Δ+23Δ2=83Δ2=43Δ
Step 4: Apply Heron's formula
According to Heron's formula, the area of the triangle can also be expressed as:
Δ=√s(s−a)(s−b)(s−c)
Substituting the values we found:
Δ=√(43Δ)(43Δ−Δ)(43Δ−Δ)(43Δ−23Δ)
This simplifies to:
Δ=√(43Δ)(13Δ)(13Δ)(23Δ)
Step 5: Simplify the expression
Calculating the terms inside the square root:
Δ=√43⋅13⋅13⋅23Δ4
=√881Δ4=2√29Δ2
Step 6: Solve for Δ
Setting the two expressions for Δ equal to each other:
Δ=2√29Δ2
Rearranging gives:
Δ2−92√2Δ=0
Factoring out Δ:
Δ(Δ−92√2)=0
Thus, we have:
Δ=0orΔ=92√2
Since the area cannot be zero, we conclude:
Δ=92√2=9√24
Final Answer
The area of triangle ABC is 9√24.
---
- hb=2 (altitude from vertex B to side AC)
- hc=3 (altitude from vertex C to side AB)
Δ=12×a×ha=12×a×2=a
(Equation 1)
Δ=12×b×hb=12×b×2=b
(Equation 2)
Δ=12×c×hc=12×c×3=32c
(Equation 3)
- From Equation 2: b=Δ
- From Equation 3: c=23Δ
s=a+b+c2=Δ+Δ+23Δ2=2Δ+23Δ2=63Δ+23Δ2=83Δ2=43Δ
Δ=√s(s−a)(s−b)(s−c)
Δ=√(43Δ)(43Δ−Δ)(43Δ−Δ)(43Δ−23Δ)
Δ=√(43Δ)(13Δ)(13Δ)(23Δ)
Δ=√43⋅13⋅13⋅23Δ4
=√881Δ4=2√29Δ2
Δ=2√29Δ2
Δ2−92√2Δ=0
Factoring out Δ:
Δ(Δ−92√2)=0
Δ=0orΔ=92√2
Δ=92√2=9√24
The area of triangle ABC is 9√24.
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.6
6 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.7
4 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.4
5 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Archives(Matrix Match Type)
1 Videos
Similar Questions
Knowledge Check
In the figure, what is the area of ΔABC?
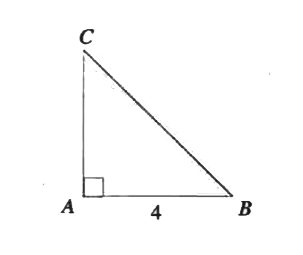 A6B7C8DIt cannot be determined from the information given
A6B7C8DIt cannot be determined from the information givenIn the figure, what is the area of ΔABC?
 A2B√2C1D1/2
A2B√2C1D1/2
Altitudes the perpendiculars drawn from the vertices of a triangle to the opposite side are known as the altitudes of the triangle.
View SolutionLet 'l' is the length of median from the vertex A to the side BC of a ΔABC. Then
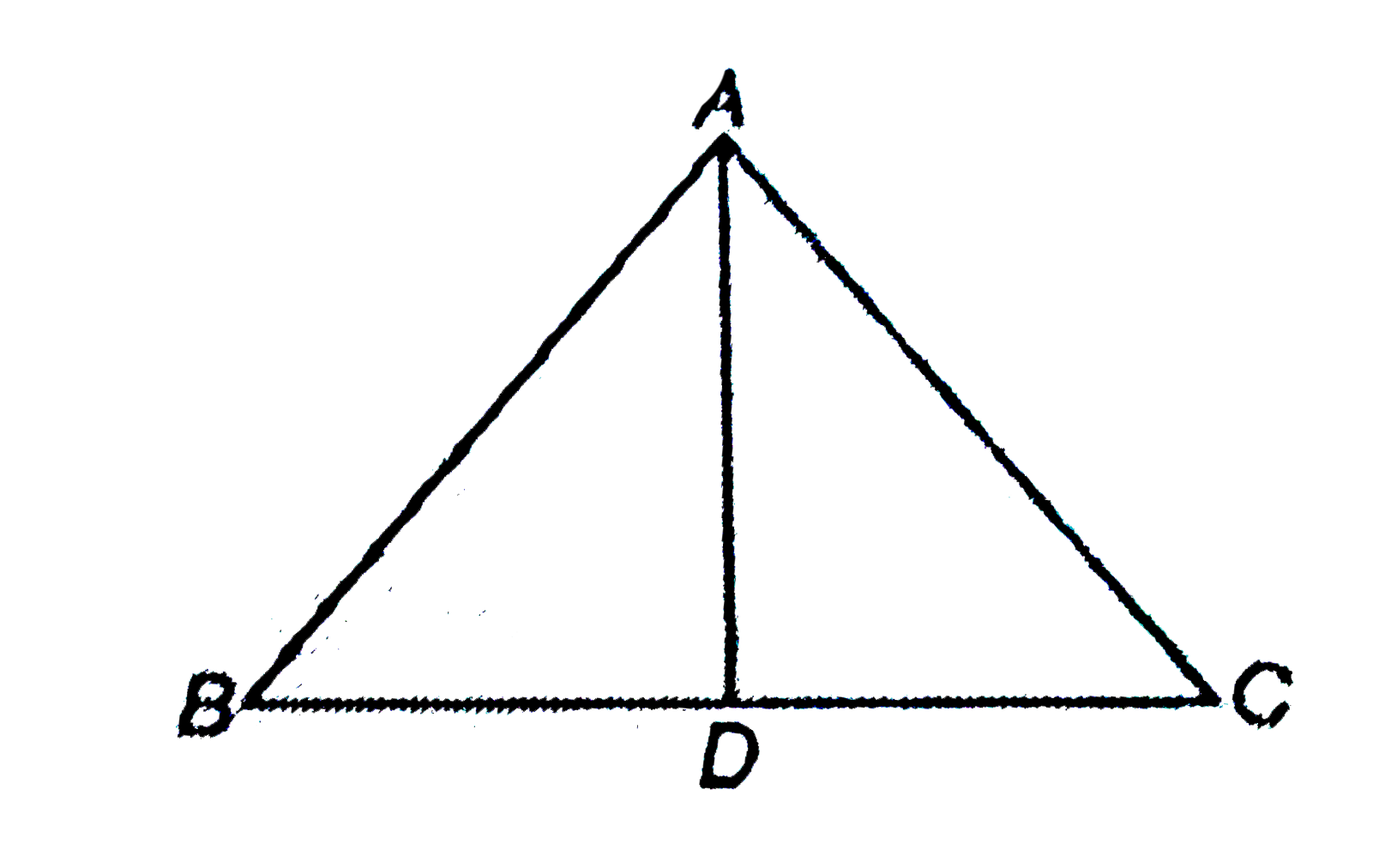
View SolutionIn the given figure AD is the median. If the area of ΔABD=10cm2, find the area of ΔABC
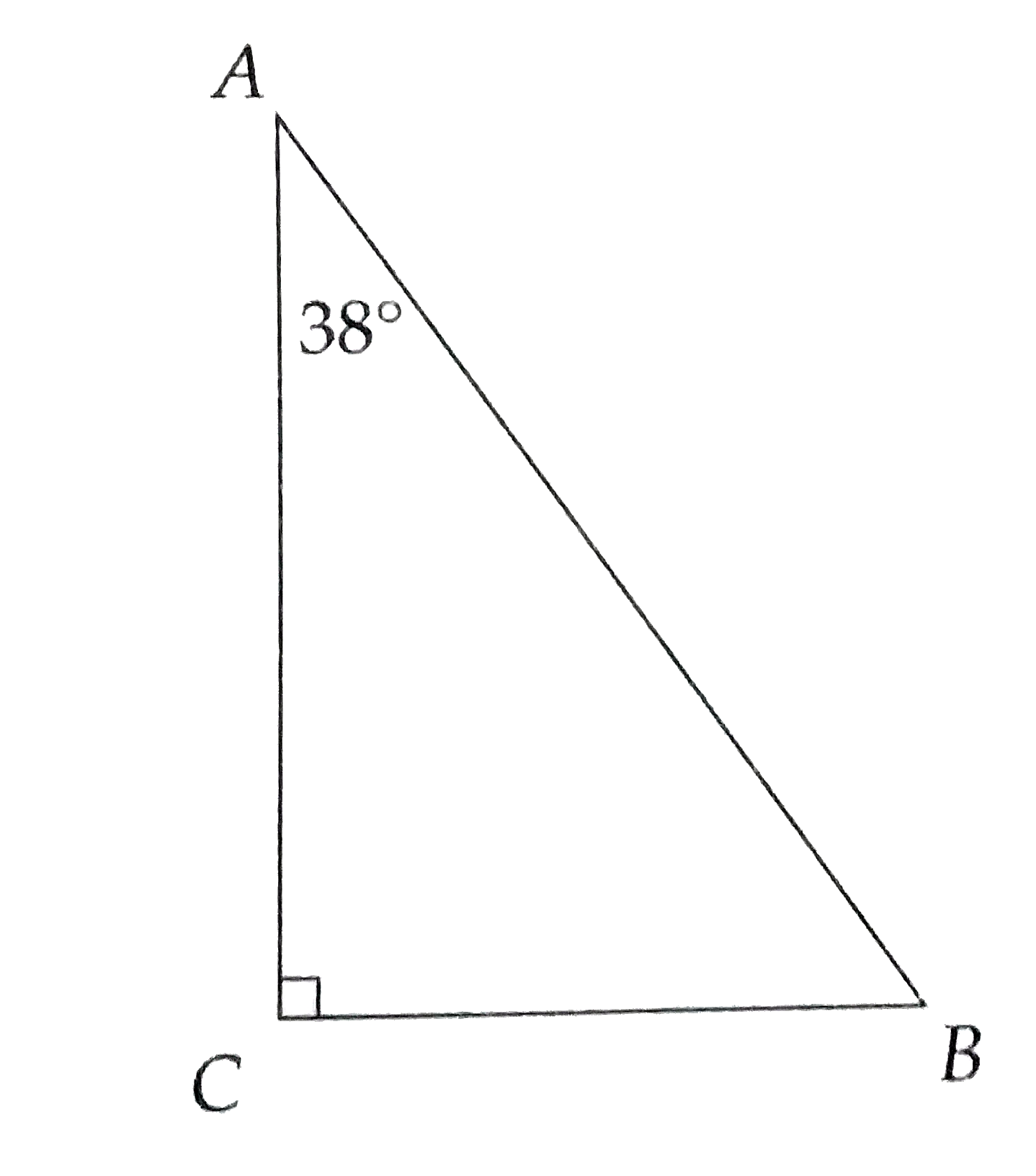
View SolutionIf the area of triangle ABC is 15, what is the length of AC ?
View SolutionIn ΔABC, E is mid-point of side AB and EBCD is a parallelogram. If the area of ΔABC is 80 cm, find the area of parallelogram EBCD.
View SolutionThe medians of ΔABC intersect at point G. Prove that:
area of ΔAGB=13× area of ΔABC
View Solution
