Regular pentagons are inscribed in two circles of radius 5and 2 units respectively. The ratio of their areas is
The correct Answer is:25:4
To find the ratio of the areas of two regular pentagons inscribed in circles of radius 5 units and 2 units respectively, we can follow these steps:
1. Understand the Area Formula for a Regular Pentagon:
The area A of a regular pentagon inscribed in a circle of radius r can be calculated using the formula:
A=52r2sin(72∘)
where r is the radius of the circumscribed circle.
2. Calculate the Area of the First Pentagon:
For the first pentagon inscribed in the circle of radius r1=5:
A1=52(52)sin(72∘)=52⋅25⋅sin(72∘)=1252sin(72∘)
3. Calculate the Area of the Second Pentagon:
For the second pentagon inscribed in the circle of radius r2=2:
A2=52(22)sin(72∘)=52⋅4⋅sin(72∘)=10sin(72∘)
4. Find the Ratio of the Areas:
To find the ratio of the areas A1A2:
A1A2=1252sin(72∘)10sin(72∘)
The sin(72∘) cancels out:
A1A2=125/210=12520=254
5. Conclusion:
The ratio of the areas of the two regular pentagons is:
A1A2=254
The area A of a regular pentagon inscribed in a circle of radius r can be calculated using the formula:
A=52r2sin(72∘)
where r is the radius of the circumscribed circle.
For the first pentagon inscribed in the circle of radius r1=5:
A1=52(52)sin(72∘)=52⋅25⋅sin(72∘)=1252sin(72∘)
For the second pentagon inscribed in the circle of radius r2=2:
A2=52(22)sin(72∘)=52⋅4⋅sin(72∘)=10sin(72∘)
To find the ratio of the areas A1A2:
A1A2=1252sin(72∘)10sin(72∘)
The sin(72∘) cancels out:
A1A2=125/210=12520=254
The ratio of the areas of the two regular pentagons is:
A1A2=254
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercises
80 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Multiple correct answer type
24 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.10
8 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Archives(Matrix Match Type)
1 Videos
Similar Questions
Knowledge Check
Find the area of a circle of radius 5.6 cm.
A58.56cm2.B78.56cm2.C98.56cm2.D88.56cm2.Shown below is a regular hexagon inscribed in a circle whose radius is 4 inches . What is the perimeter, in inches, of the hexagon?
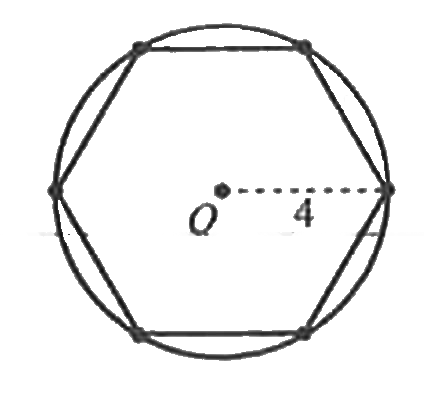 A8πB12√3C18D24
A8πB12√3C18D24
The area of the square that can be inscribed in a circle of radius 8 cm is
View SolutionThe area of an equilateral triangle inscribed in a circle of radius 4cm, is
View SolutionRectangles are inscribed inside a semi-circle of radius r. Find the rectangle with maximum area.
View SolutionIn Figure, ABC is an equilateral triangle inscribed in a circle of radius 4 cm with centre O . Find the area of the shaded region.
View SolutionIf In is the area of n sided regular polygon inscribed in a circle of unit radius and On be the area of the polygon circumscribing the given circle, prove that In=On2⎛⎝1+⎛⎝√1−(2Inn)2⎞⎠
View SolutionA reactangle with one side 4 cm is inscribed in a circle of radius 2.5 cm. Find the area of the rectangle
View Solution
