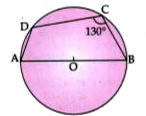
In the given figure, AB is the diameter of the circle, centered at O. If ∠COA=60∘,AB=2r,Ac=dandCD=l, then l is equal to
d√3
d/√3
3d
√3d/2
The correct Answer is:A

AC=d,OA=OBr,CD=BD=I,∠COA=π3
Clearly ΔAOC is equilateral
∴d=r
Also, ∠BOD=∠COD=2π3×2=π3
or tan.π3=BDOB=lr⇒l=r√3=d√3
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Multiple correct answer type24videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Linked comprehension type34videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.114videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )1videos
PROGRESSION AND SERIES
- BOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Archives(Matrix Match Type)1videos
RELATIONS AND FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
In the figure, AB and CD are the diameters of the circle. What is the value of x?
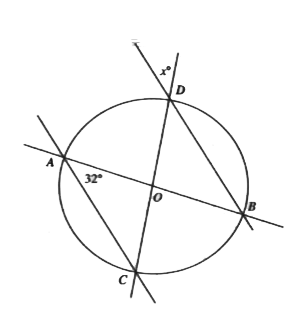 A16∘B18∘C26∘D32∘
A16∘B18∘C26∘D32∘
In the given figure, AB is the diameter of a circle with centre O.
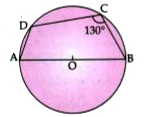
∠BCD=130∘. Find
(ii) ∠DBAView SolutionIn the given figure, AB and XY are diameters of a circle with centre O. If ∠APX=30∘, find:
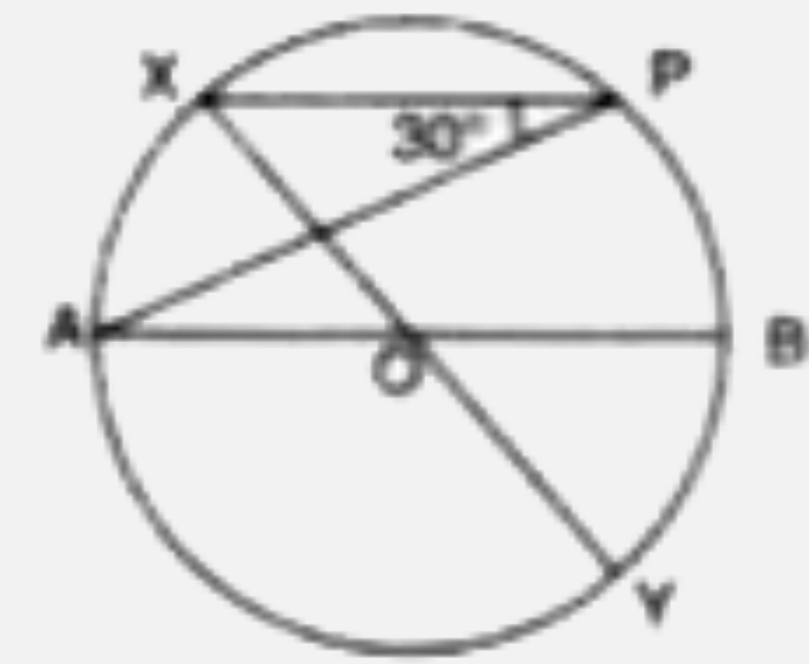
∠OAXView SolutionIn the given figure, AB and XY are diameters of a circle with centre O. If ∠APX=30∘, find:

∠BPYView SolutionIn the given figure, AB and XY are diameters of a circle with centre O. If ∠APX=30∘, find:
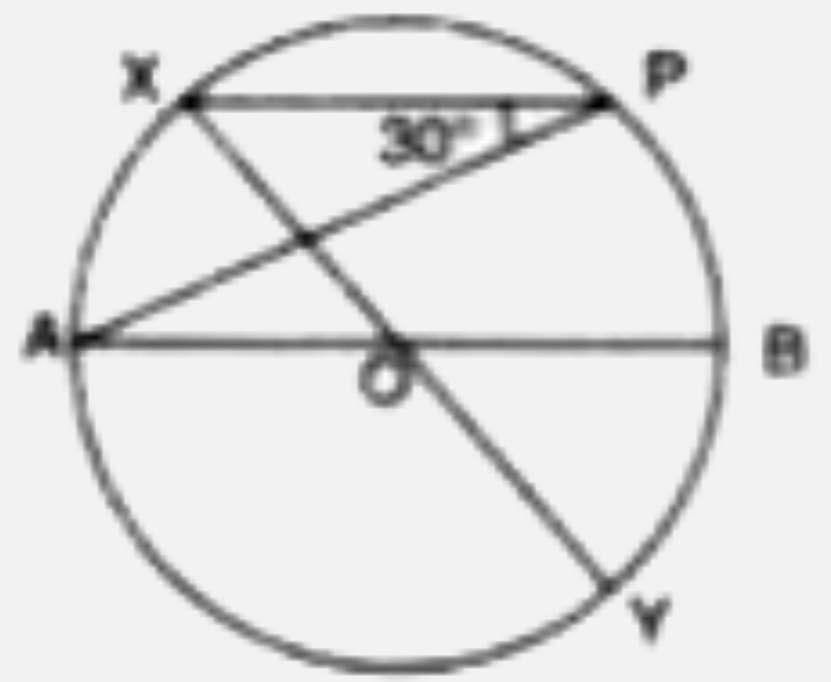
∠AOXView SolutionIn the given figure, AB and XY are diameters of a circle with centre O. If ∠APX=30∘, find:

∠APYView SolutionIn the given figure, ∠COB=40∘,AB is the diameter of the circle. Find ∠CAB:
 View Solution
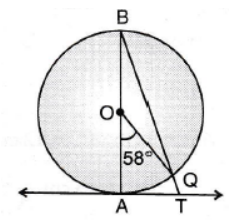
View SolutionIn the given figure, AB is diameter of a circle with centre O and AT is a tangent at ∠AOQ=58∘, find ∠ATQ.
 View Solution
View Solution