In the given figure is equilateral on side AB produced. We choose a point such that A lies between P and B. We now denote 'a' as the length of sides of , as the radius of incircle and as the ex-radius of with respect to side BC. Then is equal to
(a)
(b)
(c)
(d)
The correct Answer is:C
To solve the problem, we need to find the sum of the inradius r1 of triangle PAC and the exradius r2 of triangle PBC with respect to side BC.
1. Understanding the Geometry:
- We have an equilateral triangle ΔABC with side length a.
- Point P is chosen such that A lies between P and B.
2. Identifying the Radii:
- r1 is the radius of the incircle of triangle PAC.
- r2 is the radius of the excircle of triangle PBC opposite to side BC.
3. Using Properties of Triangles:
- For any triangle, the radius of the incircle r can be calculated using the formula:
r=As
where A is the area of the triangle and s is the semi-perimeter.
- The exradius ra opposite to side a can be calculated using:
ra=Asa
where sa is the semi-perimeter of the triangle excluding side a.
4. Calculating Areas:
- The area A of triangle ABC can be calculated as:
A=√34a2
- For triangle PAC, the area can be calculated based on the lengths of sides PA, AC, and PC.
- For triangle PBC, the area can be calculated similarly.
5. Calculating Semi-perimeters:
- The semi-perimeter s of triangle PAC is:
s=PA+AC+PC2
- The semi-perimeter sb of triangle PBC is:
sb=PB+BC+PC2
6. Finding r1 and r2:
- Substitute the areas and semi-perimeters into the formulas to find r1 and r2.
7. Summing the Radii:
- Finally, compute r1+r2.
8. Final Result:
- After performing the calculations, we find that:
r1+r2=√3⋅α2
- Here, α is the length of the side of triangle ABC.
Conclusion:
The final answer is:
r1+r2=√3⋅a2
- We have an equilateral triangle ΔABC with side length a.
- Point P is chosen such that A lies between P and B.
- r1 is the radius of the incircle of triangle PAC.
- r2 is the radius of the excircle of triangle PBC opposite to side BC.
- For any triangle, the radius of the incircle r can be calculated using the formula:
r=As
where A is the area of the triangle and s is the semi-perimeter.
- The exradius ra opposite to side a can be calculated using:
ra=Asa
where sa is the semi-perimeter of the triangle excluding side a.
- The area A of triangle ABC can be calculated as:
A=√34a2
- For triangle PAC, the area can be calculated based on the lengths of sides PA, AC, and PC.
- For triangle PBC, the area can be calculated similarly.
- The semi-perimeter s of triangle PAC is:
s=PA+AC+PC2
- The semi-perimeter sb of triangle PBC is:
sb=PB+BC+PC2
- Substitute the areas and semi-perimeters into the formulas to find r1 and r2.
- Finally, compute r1+r2.
- After performing the calculations, we find that:
r1+r2=√3⋅α2
- Here, α is the length of the side of triangle ABC.
The final answer is:
r1+r2=√3⋅a2
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Multiple correct answer type
24 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Linked comprehension type
34 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.11
4 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Archives(Matrix Match Type)
1 Videos
Similar Questions
In the given figure, ΔABC is an equilateral triangle whose side BC has been produced in both the directions to D and E respectively. Prove that ∠ACD=∠ABE.
View SolutionIf 5, 5r and 5r2 are the lengths of the sides of a triangle, then r cannot be equal to
View SolutionThe incircle of ΔABC touches side BC at D. The difference between BD and CD (R is circumradius of ΔABC) is
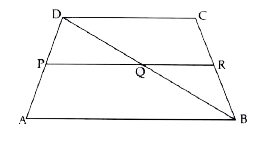
View SolutionIn the given figure ABCD is a trapezium, P is the mid-point of side AD and PR||AB||DC.
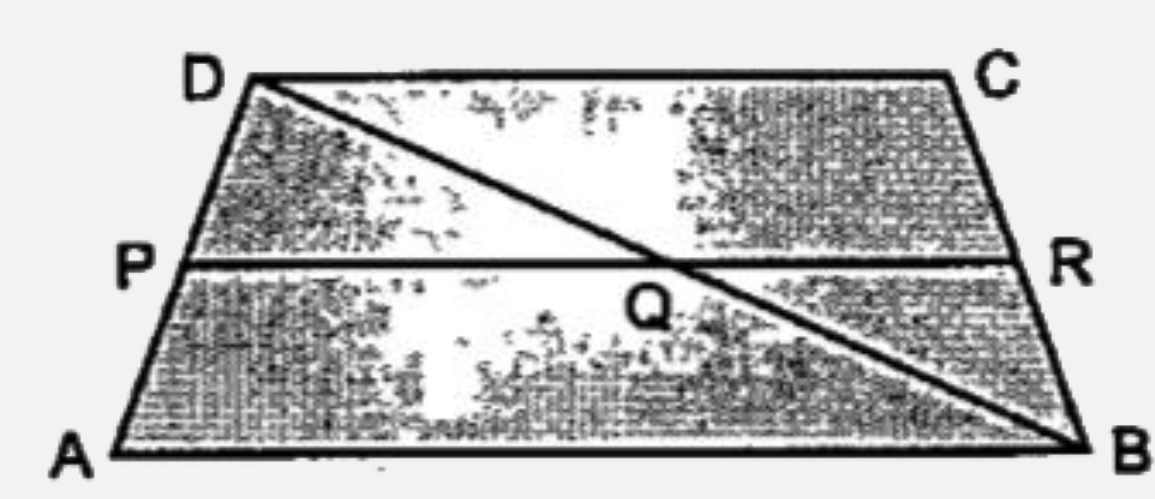
Prove that R is the mid-point of side BC
View SolutionIn the given figure ABCD is trapezium, P is the mid-point of side AD and PR||AB||DC.
(i) Prove that R is the mid-point of side BC
(ii) Find the length of PR, if AB = 12 cm and DC = 8 cm
View SolutionABC is an equilateral triangle of side 4cm. If R,randh are the circumradius, inradius, and altitude, respectively, then R+rh is equal to
View SolutionIf R denotes circumradius, then in ΔABC,b2−c22aR is equal to
View SolutionIf a right angled ΔABC of maximum area is inscribled within a circle of radius R, then (δ representes area of ΔABCandr,r1,r2,r3 represent in-radius and ex-radii, and s is the semi-perimeter of ΔABC, then
View SolutionIn the given figure the sides AB, BE and CA of triangle ABC touch a circle with centre O and radius r at P,Q and R respectively.
Prove that : (i)AB+CQ=AC+BQ

View SolutionIn ΔABC, equation of side BC is x+y-6=0, also the circumcentre and orhtocentre are (3, 1) and (2, 2) respectively, then the equation of the circumcircle of ΔABC is
View Solution
