Given an isoceles triangle with equal side of length b and angle α<π/4, then
the distance between circumcenter O and incenter I is
∣∣∣bcos(3α/2)2sinαcos(α/2)∣∣∣
∣∣∣bcos3αsin2α∣∣∣
∣∣∣bcos3αcosαsin(α/2)∣∣∣
∣∣∣bsinαcosα/2∣∣∣
The correct Answer is:A
To find the distance between the circumcenter O and incenter I of an isosceles triangle ABC with equal sides of length b and angle α<π4, we can follow these steps:
1. Identify the Triangle Properties:
- Given an isosceles triangle ABC where AB=AC=b and ∠ABC=∠ACB=α.
- The angle ∠A can be expressed as ∠A=π−2α.
Hint: Remember that in an isosceles triangle, the base angles are equal.
2. Determine the Height:
- Let AD be the altitude from A to BC. This altitude bisects BC at point D.
- Using trigonometry, we can find the length of AD as:
AD=bsin(α)
- The length of BD (half of the base) is:
BD=bcos(α)
Hint: Use the sine and cosine definitions for the right triangle ABD.
3. Calculate the Area Δ:
- The area Δ of triangle ABC can be calculated using:
Δ=12×base×height=12×BC×AD
- The length of BC is 2BD=2bcos(α), thus:
Δ=12×(2bcos(α))×(bsin(α))=b2cos(α)sin(α)
Hint: The area can also be calculated using the formula Δ=12absin(C).
4. Calculate the Semi-perimeter s:
- The semi-perimeter s of triangle ABC is given by:
s=AB+AC+BC2=b+b+2bcos(α)2=b(1+cos(α))
Hint: The semi-perimeter is half the sum of all sides.
5. Find the Circumradius R:
- Using the sine rule, the circumradius R is given by:
R=abc4Δ
- Here, a=2bcos(α), b=b, c=b, thus:
R=(2bcos(α))(b)(b)4(b2cos(α)sin(α))=bcos(α)2sin(α)
Hint: The circumradius can also be found using R=a2sin(A).
6. Find the Inradius r:
- The inradius r can be calculated as:
r=Δs=b2cos(α)sin(α)b(1+cos(α))=bcos(α)sin(α)1+cos(α)
Hint: The inradius is the area divided by the semi-perimeter.
7. Calculate the Distance d=|O−I|:
- The distance between the circumcenter O and incenter I can be expressed as:
d=|R−rcos(π−2α2)|
- Plugging in the values of R and r:
d=∣∣∣bcos(α)2sin(α)−bcos(α)sin(α)(1+cos(α))cos(α)∣∣∣
Hint: The distance formula involves the circumradius and inradius, adjusted for the angles.
8. Final Simplification:
- After substituting and simplifying, we arrive at the final expression for the distance d.
Hint: Keep track of trigonometric identities to simplify the final expression.
Final Answer:
The distance between the circumcenter O and incenter I is given by the derived expression after simplification.
- Given an isosceles triangle ABC where AB=AC=b and ∠ABC=∠ACB=α.
- The angle ∠A can be expressed as ∠A=π−2α.
- Let AD be the altitude from A to BC. This altitude bisects BC at point D.
- Using trigonometry, we can find the length of AD as:
AD=bsin(α)
- The length of BD (half of the base) is:
BD=bcos(α)
- The area Δ of triangle ABC can be calculated using:
Δ=12×base×height=12×BC×AD
- The length of BC is 2BD=2bcos(α), thus:
Δ=12×(2bcos(α))×(bsin(α))=b2cos(α)sin(α)
- The semi-perimeter s of triangle ABC is given by:
s=AB+AC+BC2=b+b+2bcos(α)2=b(1+cos(α))
- Using the sine rule, the circumradius R is given by:
R=abc4Δ
- Here, a=2bcos(α), b=b, c=b, thus:
R=(2bcos(α))(b)(b)4(b2cos(α)sin(α))=bcos(α)2sin(α)
- The inradius r can be calculated as:
r=Δs=b2cos(α)sin(α)b(1+cos(α))=bcos(α)sin(α)1+cos(α)
- The distance between the circumcenter O and incenter I can be expressed as:
d=|R−rcos(π−2α2)|
- Plugging in the values of R and r:
d=∣∣∣bcos(α)2sin(α)−bcos(α)sin(α)(1+cos(α))cos(α)∣∣∣
- After substituting and simplifying, we arrive at the final expression for the distance d.
The distance between the circumcenter O and incenter I is given by the derived expression after simplification.
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Matrix match type
6 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Numerical value type
22 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Multiple correct answer type
24 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Archives(Matrix Match Type)
1 Videos
Similar Questions
Knowledge Check
In a triangle with sides of lengths 3,4, and 5, the smallest angle is 37.87∘. In the figure, O is the center of the circle of radius 5. A and B are two points on the circle , and the distance between the points is 6. what is the value of x?
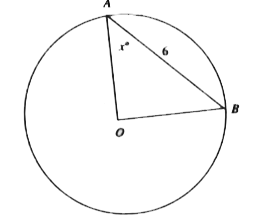 A36.87B45C53.13D116.85
A36.87B45C53.13D116.85
Given an isosceles triangle with lateral side of length b, base angle α<π4,R,r the radii and O, I the centres of the circumcircle and incircle respectively, then prove that: OI=∣∣ ∣∣bcos,3α22sinαcos,α2∣∣ ∣∣
View SolutionGiven an isosceles triangle with lateral side of length b, base angle α<π4,R,r the radii and O, I the centres of the circumcircle and incircle respectively, then prove that: r=bsin2α2(1+cosalopha)
View SolutionDraw an isosceles triangle in which each of the equal sides is of length 3 cm and the angle between them is450.
View SolutionProve that the distance between the circumcenter and the incenter of triangle ABC is√R2−2Rr
View SolutionConstruct an isosceles triangle with each of its equal sides equal to 6 cm and the angle between them equal to 70∘.
View SolutionIn triangle ABC,letR=circumradius,r=inradius. If r is the distance between the circumcenter and the incenter, the ratio Rr is equal to (a)√2−1 (b) √3−1 (c)√2+1 (d) √3+1
View SolutionIf in an isosceles triangle with base 'a', vertical angle 20∘ and lateral side each of length 'b' is given then value of a3+b3 equals
View Solution
