Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are 90∘−12A,90∘−12B and 90∘−12C
2Rcos.A2
2Rsin(A2)
Rcos(A2)
2Rcos(B2)cos(C2)
The correct Answer is:A
Area of ΔABC=abc4R=2R2sinAsinBsinC
∠ADE=∠ABE=B2
Similarly, ∠FDA=∠FCA=C2
⇒∠FDE=B+C2
and ∠DEF=A+C2and∠DFE=A+B2

In ΔDEF, by sine rule, EFsin(∠FDE)=2R
⇒EF=2Rcos(A2)
Then, area of ΔDEF
=2R2sin(A+B2)sin(B+C2)sin(A+C2)
=2R2cos(A2)cos(B2)cos(C2)
Now ΔABCΔDEF=2R2sinAsinBsinC2R2cos(A2)cos(B2)cos(C2)
=8sin(A2)sin(B2)sin(C2)≤1
⇒ΔABC≤ΔDEF
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Matrix match type
6 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Numerical value type
22 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Multiple correct answer type
24 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Archives(Matrix Match Type)
1 Videos
Similar Questions
Bisectors of angles A, B and C of a triangle ABC intersect its circumcircle at D, E and F respectively. Prove that the angles of the triangle DEF are 90o−12A ,90o−12B and 90o−12C
View SolutionBisectors of vertex angles A, B and C of a triangle ABC intersect its circumcircle at the points D,E and F respectively. Prove that angle EDF=90∘−12∠A
View SolutionThe bisectors of the angles B and C of a triangle ABC , meet the opposite sides in D and E respectively. If DE||BC , prove that the triangle is isosceles.
View SolutionIn ABC, the three bisectors of the angle A, B and C are extended to intersect the circumcircle at D,E and F respectively. Prove that ADcosA2+BEcosB2+CFcosC2=2R(sinA+sinB+sinC)
View SolutionIf the bisector of the angel C of a triangle ABC cuts AB in D and the circumcircle E, prove that CE:DE=(a+b)2:c2
View SolutionLet the altitudes from the vertices A, B and Cof the triangle e ABCmeet its circumcircle at D, E and F respectively and z1,z2andz3 represent the points D, E and F respectively. If z3−z1z2−z1 is purely real then the triangle ABC is
View SolutionThe angles A, B and C of a triangle ABC are in arithmetic progression. If 2b2=3c2 then the angle A is :
View SolutionBisectors of interior ∠ B and exterior ∠ ACD of a ΔABC intersect at the point T. prove that ∠BTC=12∠ BAC.
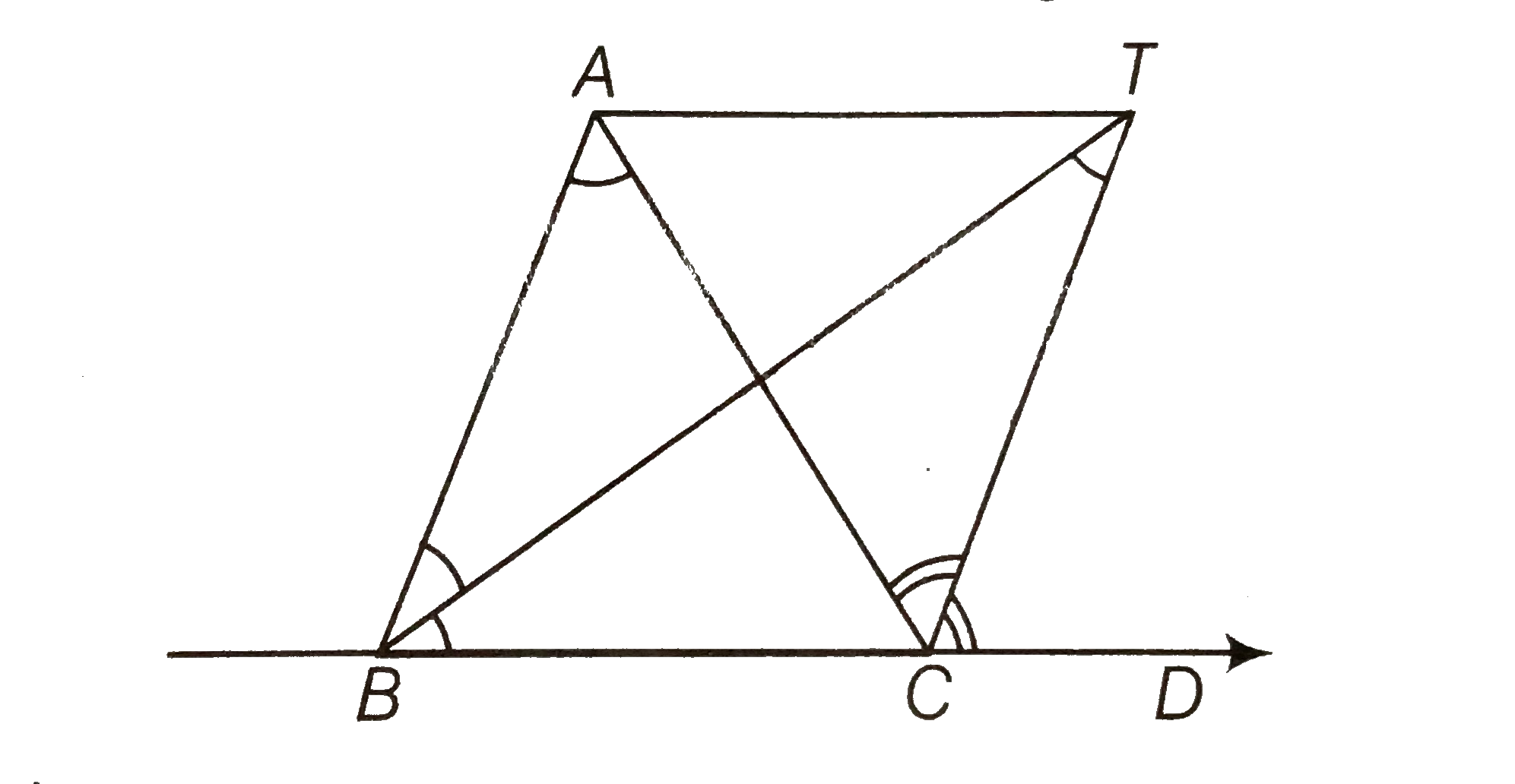
View SolutionThe internal bisectors of the angles of a triangle ABC meet the sides in D, E, and F. Show that the area of the triangle DEF is equal to 2△abc(b+c)(c+a)(a+b), where △ is the area of ABC.
View SolutionThe circumcentre of the triangle ABC is O . Prove that ∠OBC+∠BAC=90∘.
View Solution
