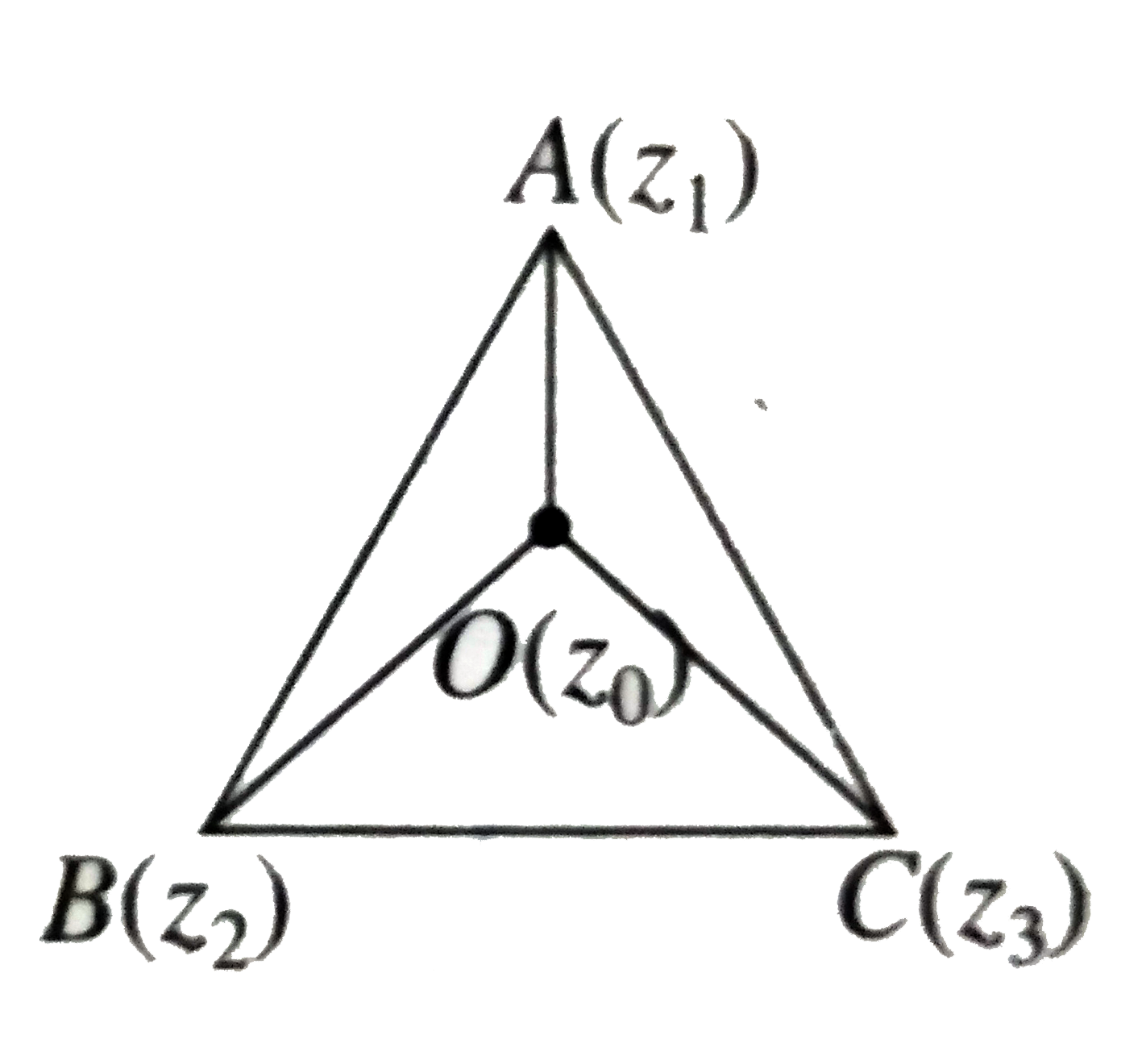
If z1, z2 and z3 are the vertices of ΔABC, which is not right angled triangle taken in anti-clock wise direction and z0 is the circumcentre, then (z0−z1z0−z2)sin2Asin2B+(z0−z3z0−z2)sin2Csin2B is equal to
0
1
−1
2
The correct Answer is:C
(c) Takin rotation at 'O' ltbr> z0−z1z0−z2=cos2C−isin2C
z0−z3z0−z2=cos2A+isin2A
Now (z0−z1z0−z2)sin2Asin2B+(z0−z3z0−z2)sin2Csin2B
=sin2Acos2C−isin2Asin2C
=+cos2Asin2C+isin2Asin2Csin2B
=sin(2A+2C)sin2B=−1
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - Multiple Correct Answer11videos
COMPLEX NUMBERS
- BOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - Comprehension11videos
COMPLEX NUMBERS
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
- BOOK - CENGAGE ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - All Questions101videos
CONIC SECTIONS
Similar Questions
If z1,z2,z3 are the vertices of an isoscles triangle right angled at z2, then
View Solutionz1,z2,z3 are the vertices of an equilateral triangle taken in counter clockwise direction. If its circumcenter is at (1−2i) and (z1=2+i), then z2=
View Solutionz1,z2,z3 are the vertices of an equilateral triangle taken in counter clockwise direction. If its circumference is at the origin and z1=1+i, then
View SolutionIf the tangents at z1, z2 on the circle |z−z0|=r intersect at z3, then (z3−z1)(z0−z2)(z0−z1)(z3−z2) equals
View SolutionComplex numbers z1,z2andz3 are the vertices A,B,C respectivelt of an isosceles right angled triangle with right angle at C. show that (z1−z2)2=2(z1−z3)(z3−z2).
View SolutionIf z1,z2andz3 are the affixes of the vertices of a triangle having its circumcentre at the
origin. If zis the affix of its orthocentre, prove that
Z1+Z2+Z3−Z=0.View SolutionIf z1,z2andz3 are the vertices of an equilasteral triangle with z0 as its circumcentre , then changing origin to z0 ,show that z21+z22+z23=0, wherez1,z2,z3, are new complex numbers of the vertices.
View SolutionLet the complex numbers z1,z2 and z3 be the vertices of an equailateral triangle. If z0 is the circumcentre of the triangle , then prove that z21+z22+z23=3z20.
View SolutionIf arg (z1z2)=0 and |z1|=|z2|=1, then
View SolutionLet A(z1),B(z2),C(z3 and D(z4) be the vertices of a trepezium in an Argand plane such that AB∣∣CD Let |z1−z2|=4,|z3,z4|=10 and the diagonals AC and BD intersects at P. It is given that Arg(z4−z2z3−z1)=π2 and Arg(z3−z2z4−z1)=π4
Which of the following option(s) is/are correct?View Solution

