Let $P$ denotes a complex number $z = r (cos θ + i sin θ)$ on the Argand's plane, and $Q$ denotes a complex number $\sqrt{2 {| z |}^{2}} (cos (θ + \frac{π}{4}) + i sin (θ + \frac{π}{4}))$ . If $' O'$ is the origin, then $Δ O P Q$ is

A

isosceles but not right angled

B

right angled but not isosceles

C

right isosceles

D

equilateral

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$(c)$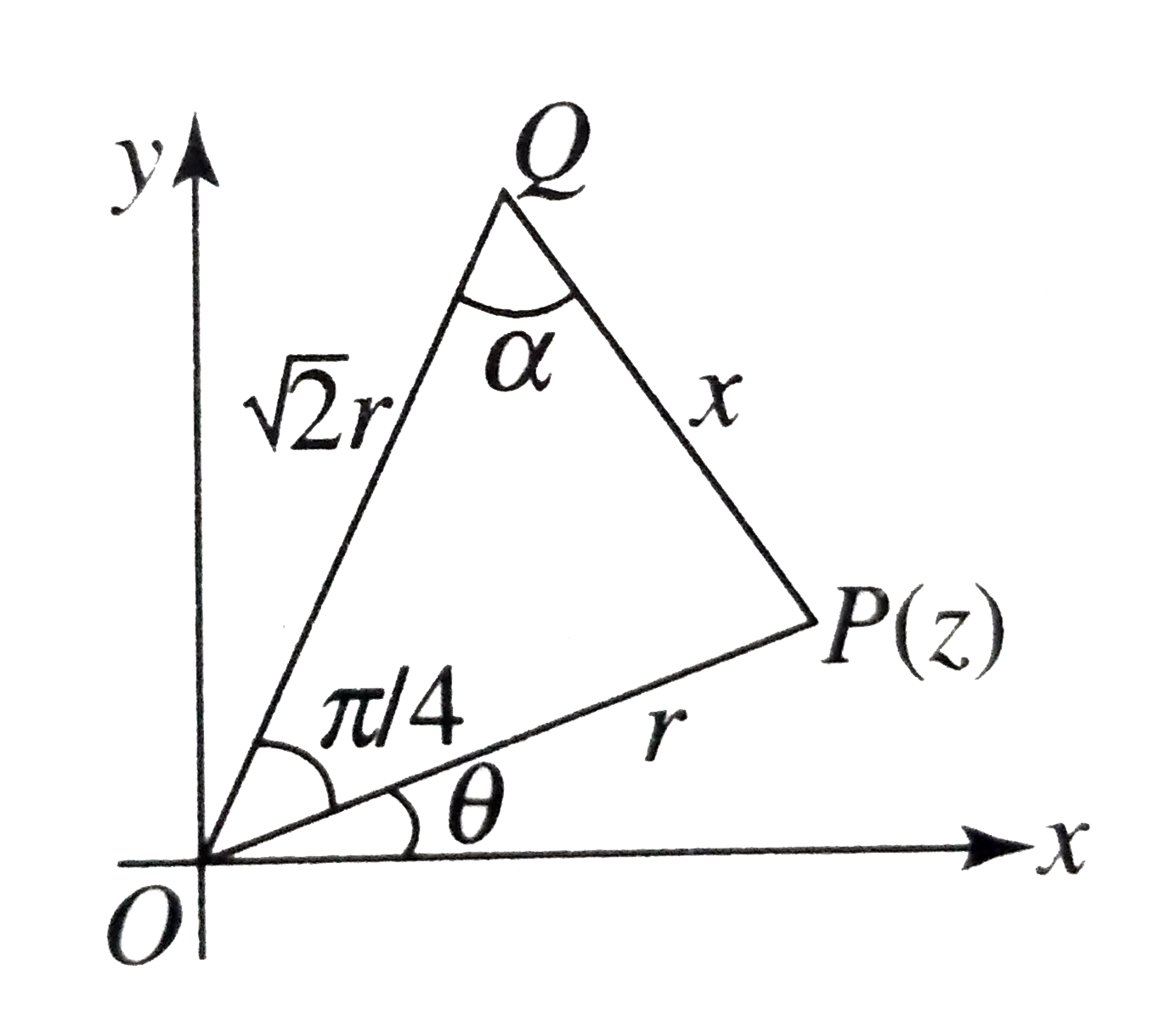
$Z_{P} = r (cos θ + i sin θ)$
$Z_{0} = \sqrt{2 {| z |}^{2}} (cos (θ + \frac{π}{4}) + i sin (θ + \frac{π}{4}))$
$= \sqrt{2} r [cos (θ + \frac{π}{4}) + i sin (θ + \frac{π}{4})]$
From the figure,
$cos \frac{π}{4} = \frac{2 r^{2} + r^{2} - x^{2}}{2 \cdot \sqrt{2 r} \cdot r} = \frac{3 r^{2} - x^{2}}{2 \sqrt{2} r^{2}}$
$∴ 1 = \frac{3 r^{2} - x^{2}}{2 r^{2}}$
$\Rightarrow r^{2} = x^{2} \Rightarrow x = r \Rightarrow$ Triangle is right isosceles.

|

Updated on:21/07/2023

Class 12 MATHS COMPLEX NUMBERS

Topper's Solved these Questions

Similar Questions

CENGAGE ENGLISH-COMPLEX NUMBERS-MATRIX MATCH TYPE

Home
Ask Doubt
Profile