The locus of any point $P (z)$ on argand plane is $a r g (\frac{z - 5 i}{z + 5 i}) = \frac{π}{4}$ .
Then the length of the arc described by the locus of $P (z)$ is

A

$10 \sqrt{2} π$

B

$\frac{15 π}{\sqrt{2}}$

C

$\frac{5 π}{\sqrt{2}}$

D

$5 \sqrt{2} π$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$(b)$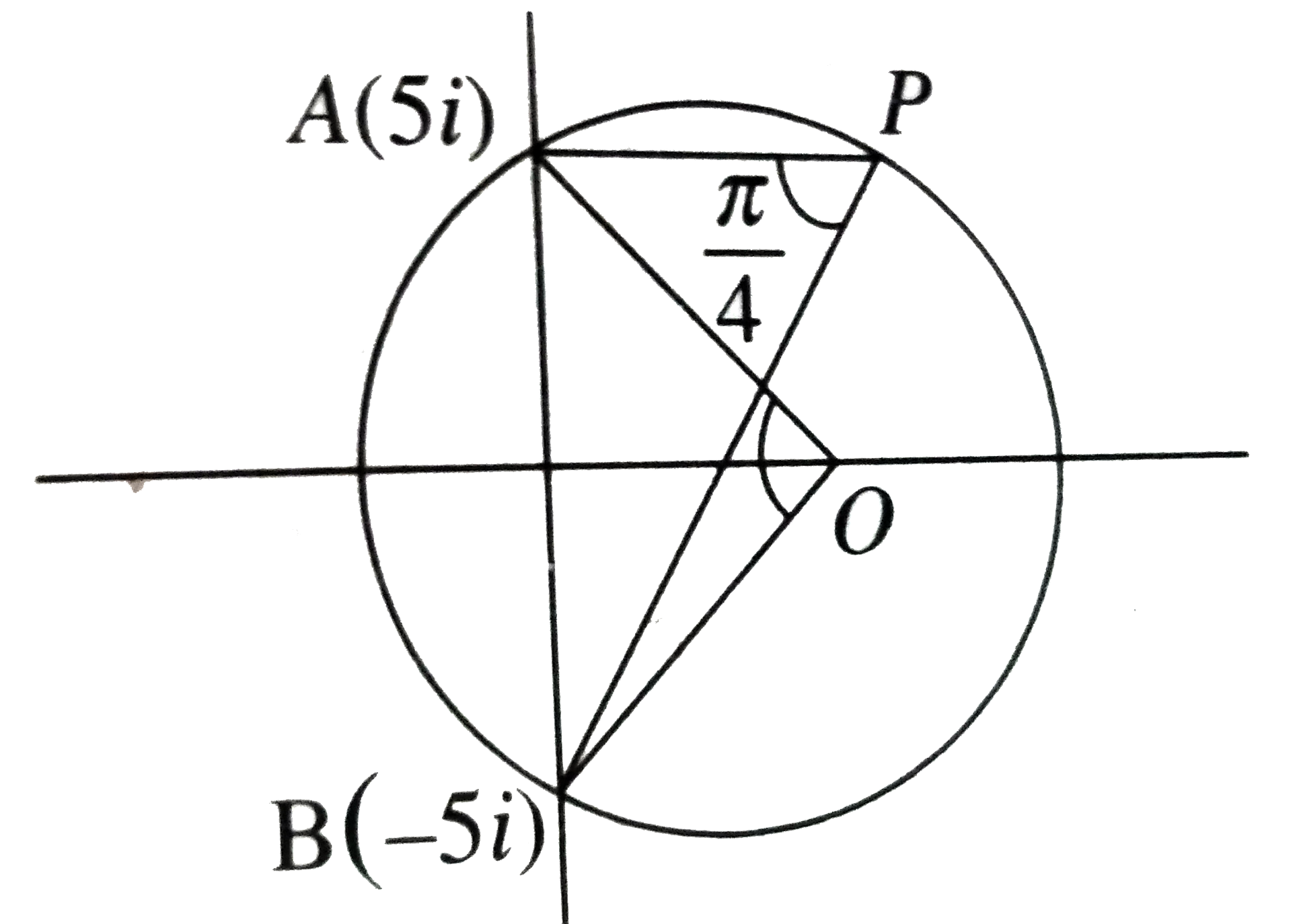
Given $∠ A P B = π / 4 \Rightarrow ∠ A O B = π / 2$
Let $O A = O B = R =$ radius of the circle
$\Rightarrow 2 R^{2} = 10^{2} \Rightarrow R = 5 \sqrt{2}$
Length of the arc $= 5 \sqrt{2} \times \frac{3 π}{2}$

|

Updated on:21/07/2023

Class 12 MATHS COMPLEX NUMBERS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If $| z - 3 + i | = 4$ , then the locus of z is
A $x^{2} + y^{2} - 6 = 0$
B $x^{2} + y^{2} - 3 x + y - 6 = 0$
C $x^{2} + y^{2} - 6 x - 2 = 0$
D $x^{2} + y^{2} - 6 x + 2 y - 6 = 0$

CENGAGE ENGLISH-COMPLEX NUMBERS-Comprehension

Home
Ask Doubt
Profile