74C37−2 is divisibl by
372
38
36
none of these
The correct Answer is:A
To solve the problem of determining by which number (7437)−2 is divisible, we can follow these steps:
Step 1: Rewrite the Binomial Coefficient
We start with the expression (7437)−2. We can express (7437) using the identity (nr)=(nn−r):
(7437)=(7437)
Step 2: Use the Binomial Theorem
According to the binomial theorem, we can express (x+y)n as:
n∑k=0(nk)xn−kyk
In our case, we can consider x=1 and y=1:
(1+1)74=74∑k=0(74k)=274
Step 3: Find the Value of (7437)
From the symmetry property of binomial coefficients, we know:
(7437)=(7437)=74!37!⋅37!
Step 4: Analyze (7437)−2
Now we need to analyze (7437)−2:
(7437)−2
Step 5: Check Divisibility by 37
Using Lucas' theorem, we can check the divisibility of (7437) by 37. Since 74 and 37 both have a digit in the base 37 representation, we can conclude that:
(7437)≡0mod37
Thus:
(7437)−2≡−2mod37
This means (7437)−2 is not divisible by 37.
Step 6: Check Divisibility by 372
Next, we check if (7437)−2 is divisible by 372. Since (7437) is divisible by 37, we can conclude:
(7437)−2≡−2mod372
This indicates that (7437)−2 is divisible by 372.
Conclusion
Thus, (7437)−2 is divisible by 372.
---
We start with the expression (7437)−2. We can express (7437) using the identity (nr)=(nn−r):
(7437)=(7437)
According to the binomial theorem, we can express (x+y)n as:
n∑k=0(nk)xn−kyk
In our case, we can consider x=1 and y=1:
(1+1)74=74∑k=0(74k)=274
From the symmetry property of binomial coefficients, we know:
(7437)=(7437)=74!37!⋅37!
Now we need to analyze (7437)−2:
(7437)−2
Using Lucas' theorem, we can check the divisibility of (7437) by 37. Since 74 and 37 both have a digit in the base 37 representation, we can conclude that:
(7437)≡0mod37
Thus:
(7437)−2≡−2mod37
This means (7437)−2 is not divisible by 37.
Next, we check if (7437)−2 is divisible by 372. Since (7437) is divisible by 37, we can conclude:
(7437)−2≡−2mod372
This indicates that (7437)−2 is divisible by 372.
Thus, (7437)−2 is divisible by 372.
Similar Questions
N2O4 is 25% dissociated at 37∘C and one atmosphere pressure. Calculate (i) Kp and (ii) the percentage dissociation at 0.1 atm and 37∘C .
View SolutionThe expression √sin4(37.5)∘+4cos2(37.5)∘+√cos4(37.5)∘+4sin2(37.5)∘ simplifies to
View SolutionThe value of ∫e371πsin(πInx)xdx is (a) 2 (b) 4 (c) e27 (d) e37
View SolutionN2O4 is 25% dissociated at 37∘C and one atmosphere pressure. Calculate (i) Kp and (ii) the percentage dissociation at 0.1 atm and 37∘C
View SolutionIf f(x)=40C1.x(1−x)39+2.40C2.x2(1−x)38+3.40C3.x3(1−x)37+…..+40.40C40.x40, then the value of f(3) is
View SolutionThe van't Hoff factor for 0.1MBa(NO3)2 solution is 2.74. The degree of dissociation is
View SolutionThe van't Hoff factor for 0.1MBa(NO3)2 solution is 2.74. The degree of dissociation is
View SolutionTwenty-two grams of CO2 at 27∘C is mixed with 16g of O2 at 37∘C. The temperature of the mixture is about
View Solutiontan46∘tan14∘−tan74∘tan14∘+tan74∘tan46∘ is equal to
View SolutionThe potential of the cell at 25∘C is
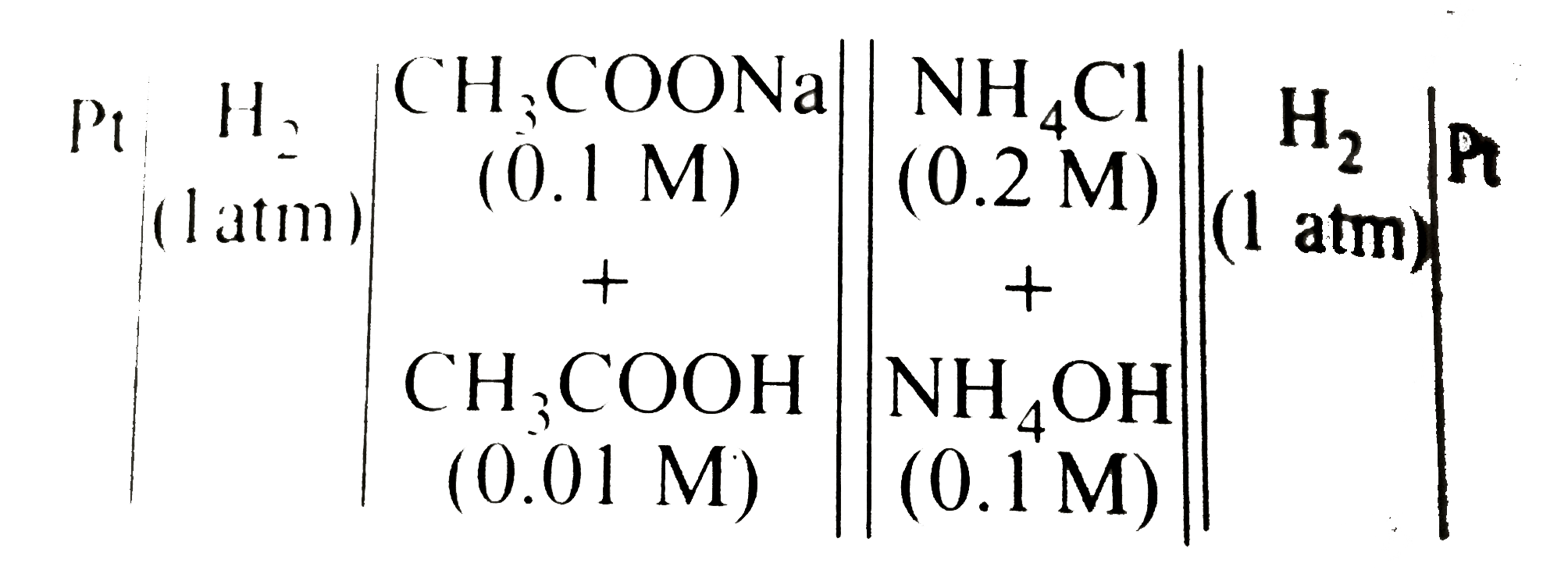
Given pKa of CH3COOH and pKb of NH4OH=4.74View Solution

