Question

Find the area bounded by the curves $y=\sin xandy=\cos x$
between two consecutive points of the intersection.

Explanation

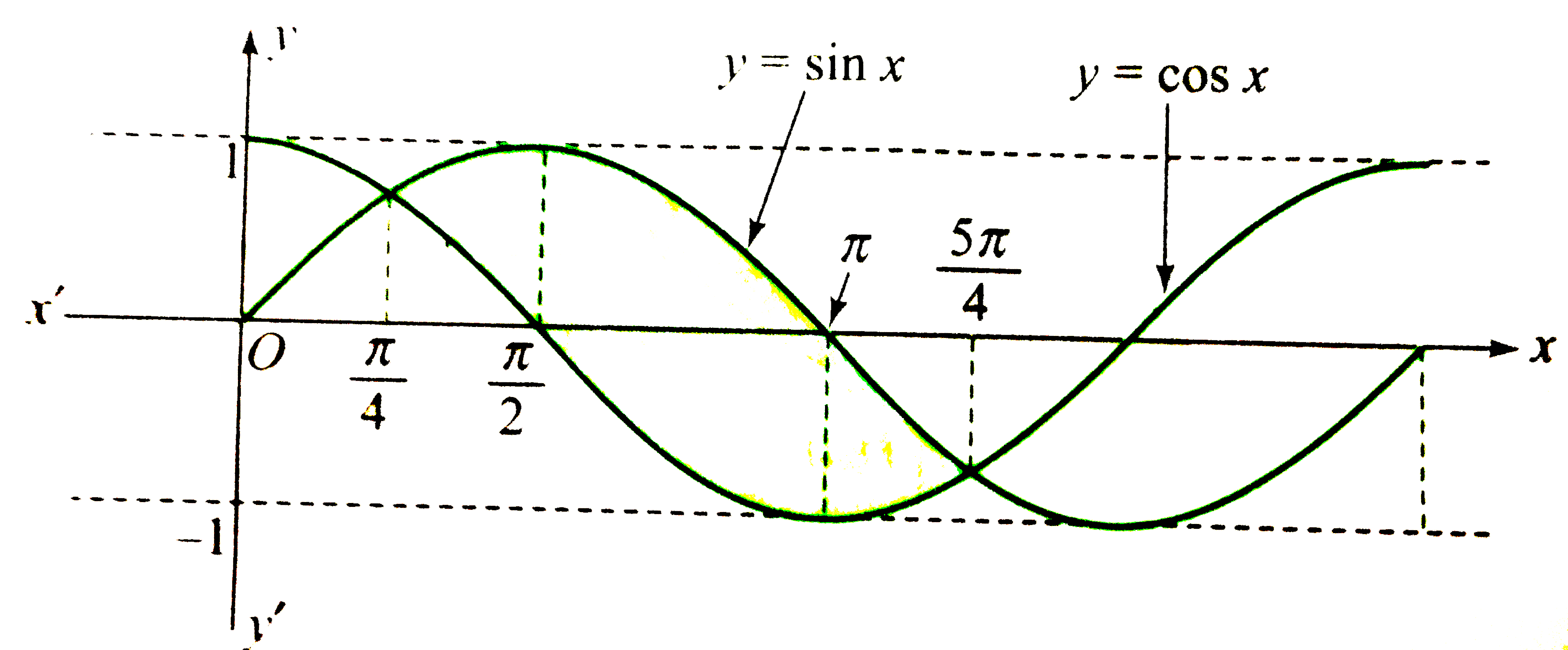
Two consecutive points of intersection of `y= sin x and y= cos x` can be taken as `x=pi//4 and x=5pi//4.` Therefore,
`"Required area "=int_(pi//4)^(5pi//4)(sin x- cos x)dx`
`=[-cos x - sin x]_(pi//4)^(5pi//4)`
`=(2)/(sqrt(2))+(2)/(sqrt(2))`
`=2sqrt(2)` sq. units