Question

Find the area of the region enclosed by the curves $y=x\log x$ and $y=2x-2x^2\stackrel{.}{}$

Explanation

Curve tracing, `y=x log_(e)x`
Clearly `xgt0`,
`"For "0lt x lt 1, x log_(e) x lt 0," and for "xgt1, x log_(e) x gt0`
`"Also "x log_(e) x = 0" for "x =1`
`"Further "(dy)/(dx)=0rArr1+ log_(e) x=0 or x=1//e,` which is point of minima.
`underset(xrarroo)lim x log_(e) x=oo.` Graph of functon is as shown in the figure.
`y=2x-2x^(2)` is downward parabola intersecting x-axis at x=0 and x=1.

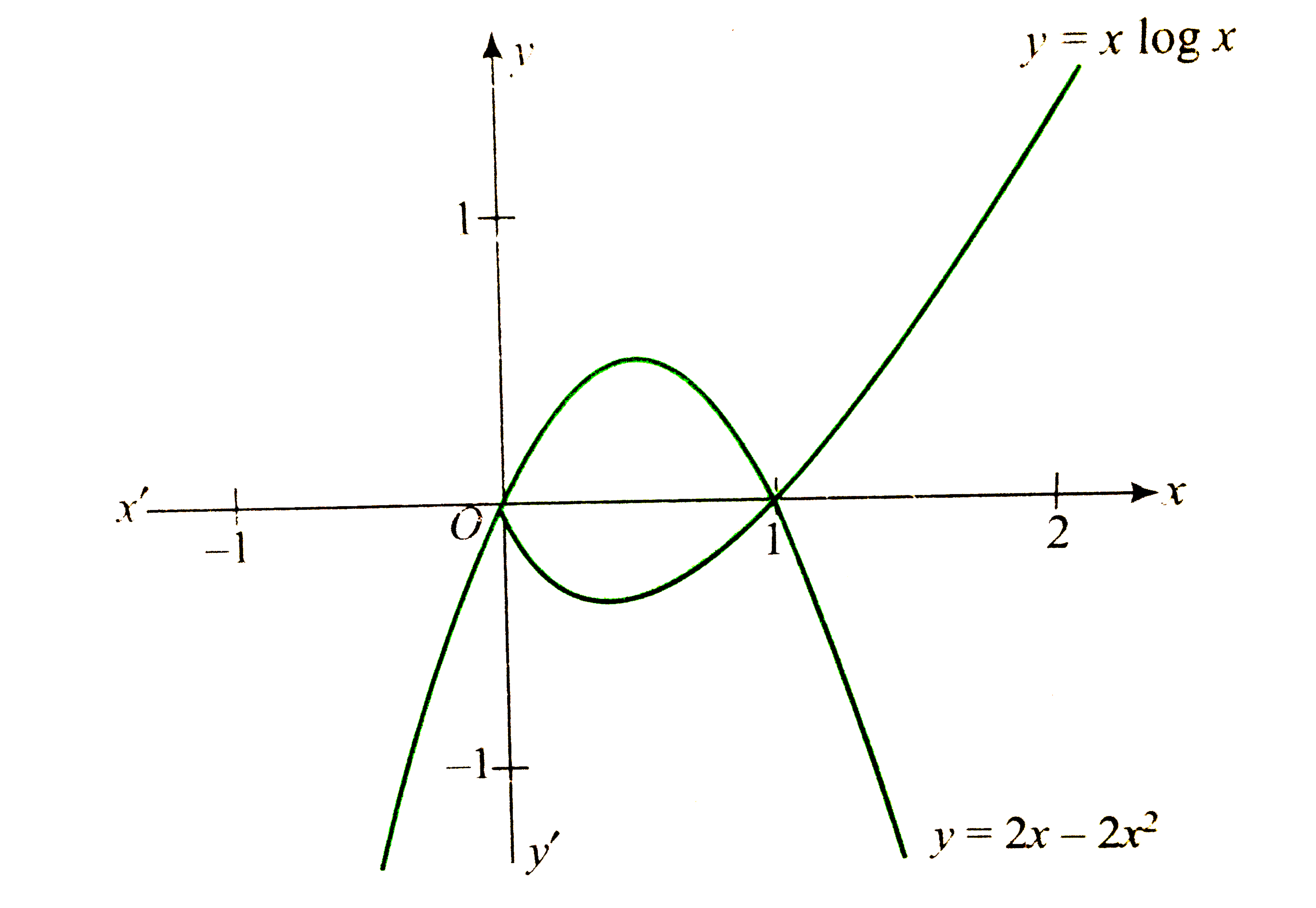
`"Required area "=overset(1)underset(0)int(2x-2x^(2))dx-overset(1)underset(0)intx log x dx `
`=[x^(2)-(2x^(3))/(3)]_(0)^(1)-[(x^(2))/(2)log x -(x^(2))/(4)]_(0)^(1)`
`(1-(2)/(3))-[0-(1)/(4)-(1)/(2)underset(xrarr0)lim x^(2) log x]=(1)/(3)+(1)/(4)=(7)/(12)`