If the area bounded by f(x)=√tanx,y=f(c),x=0andx=a,0<c<a<π2 is minimum then find the value of c.
To find the value of c that minimizes the area bounded by the curve f(x)=√tanx, the line y=f(c), and the vertical lines x=0 and x=a (where 0<c<a<π2), we can follow these steps:
Step 1: Define the Area
The area A bounded by the curve and the lines can be expressed as:
A=∫c0(f(c)−f(x))dx+∫ac(f(x)−f(c))dx
Substituting f(x)=√tanx, we have:
A=∫c0(√tanc−√tanx)dx+∫ac(√tanx−√tanc)dx
Step 2: Simplify the Area Expression
This can be simplified to:
A=c√tanc−∫c0√tanxdx+∫ac√tanxdx−(a−c)√tanc
Thus, we can rewrite the area as:
A=c√tanc−∫c0√tanxdx+∫ac√tanxdx−a√tanc+c√tanc
This simplifies to:
A=(2c−a)√tanc−∫c0√tanxdx+∫ac√tanxdx
Step 3: Differentiate the Area with Respect to c
To find the minimum area, we differentiate A with respect to c:
dAdc=2tanc+(2c−a)⋅sec2c−√tanc
Setting dAdc=0 gives us the critical points.
Step 4: Solve for c
From the derivative, we can rearrange to find:
2tanc+(2c−a)sec2c−√tanc=0
This is a complex equation, but we can analyze it further.
Step 5: Find the Minimum Value of c
To minimize the area, we observe that the area is minimized when c=a2. This is derived from the symmetry of the area under the curve and the properties of the tangent function.
Conclusion
Thus, the value of c that minimizes the area is:
a2
The area A bounded by the curve and the lines can be expressed as:
A=∫c0(f(c)−f(x))dx+∫ac(f(x)−f(c))dx
Substituting f(x)=√tanx, we have:
A=∫c0(√tanc−√tanx)dx+∫ac(√tanx−√tanc)dx
This can be simplified to:
A=c√tanc−∫c0√tanxdx+∫ac√tanxdx−(a−c)√tanc
Thus, we can rewrite the area as:
A=c√tanc−∫c0√tanxdx+∫ac√tanxdx−a√tanc+c√tanc
This simplifies to:
A=(2c−a)√tanc−∫c0√tanxdx+∫ac√tanxdx
To find the minimum area, we differentiate A with respect to c:
dAdc=2tanc+(2c−a)⋅sec2c−√tanc
Setting dAdc=0 gives us the critical points.
From the derivative, we can rearrange to find:
2tanc+(2c−a)sec2c−√tanc=0
This is a complex equation, but we can analyze it further.
To minimize the area, we observe that the area is minimized when c=a2. This is derived from the symmetry of the area under the curve and the properties of the tangent function.
Thus, the value of c that minimizes the area is:
a2
Topper's Solved these Questions
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Solved Examples
10 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Concept Application Exercise 9.1
9 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
Similar Questions
The area bounded by y=tanx,y=cotx, X-axis in 0≤x≤π2 is
View SolutionFind the area bounded by y=1+2sin2x,X-axis,X=0 and x=π.
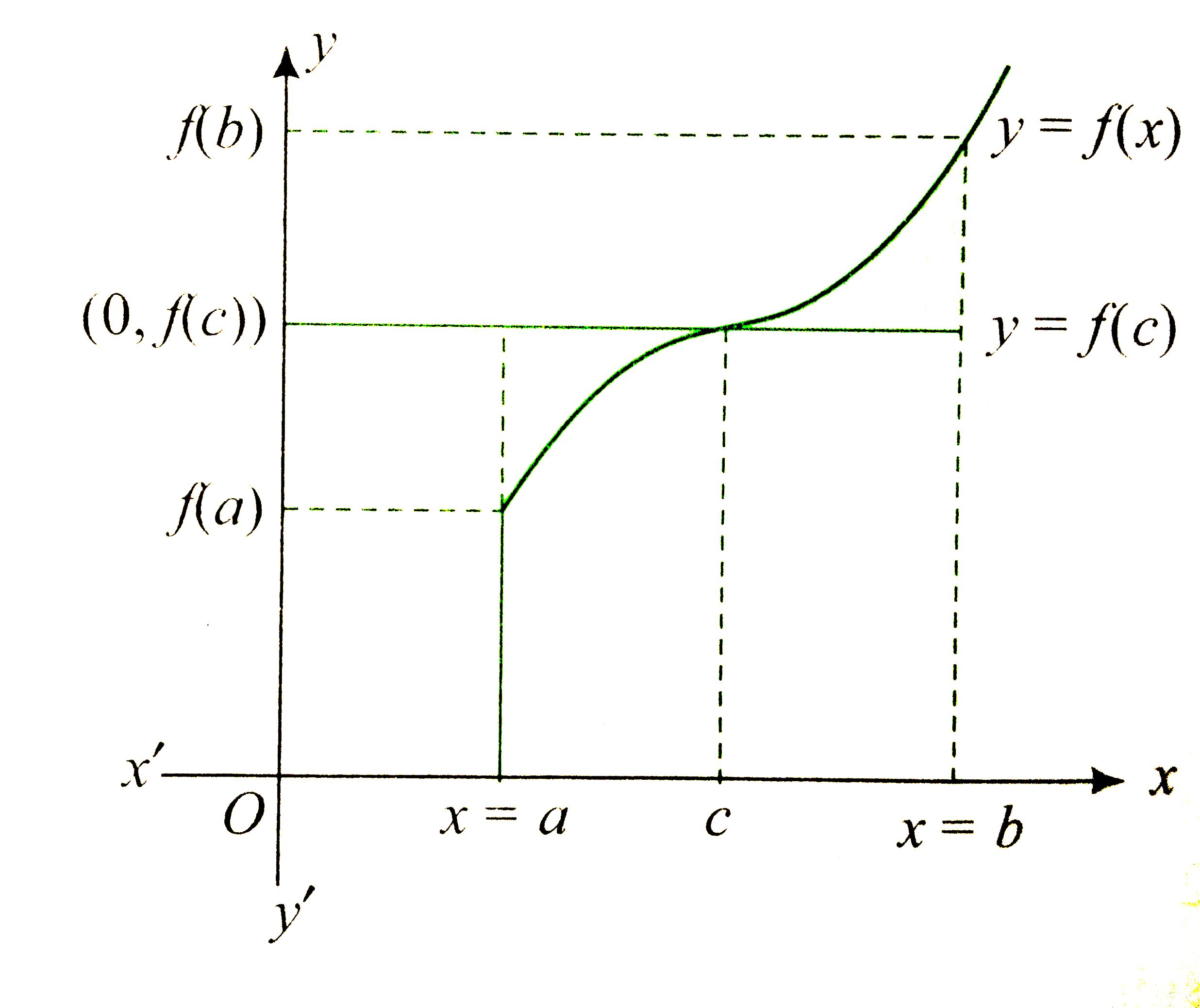
View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx
Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
If the area bounded by f(x)=x33−x2+a and the straight lines x=0, x=2, and the x-axis is minimum, then the value of a is
View SolutionFind the area bounded by y = sin x and axis of x in (0,π)
View SolutionThe area bounded by f(x)=sin−1(sinx) and
g(x)=π2−√π22−(x−π2)2 is
View SolutionFind the area bounded by the curve y=cosxbetween x=0and x=2π.
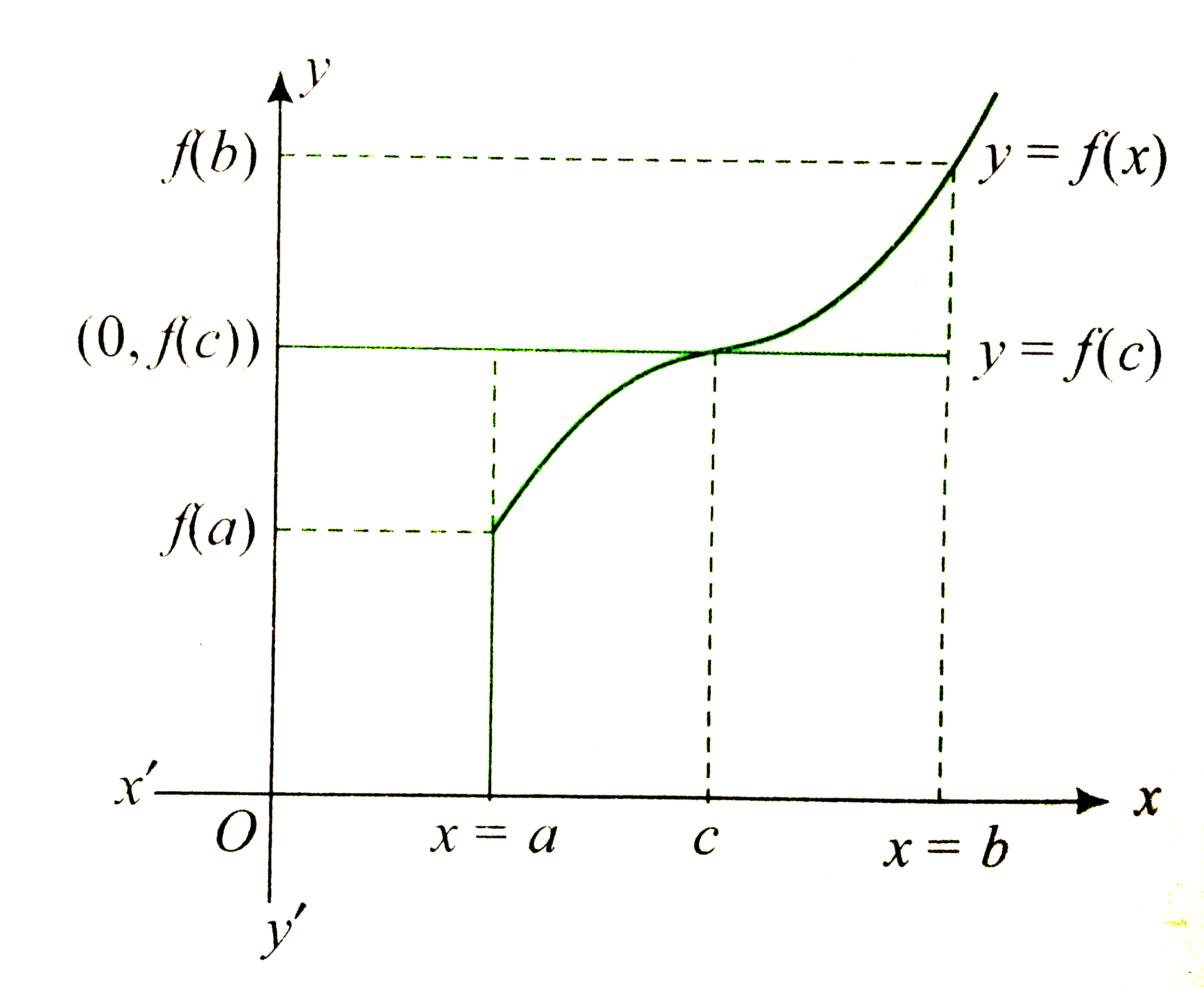
View SolutionIf y=f(x) is a monotonic function in (a,b), then the area bounded by the ordinates at x=a,x=b,y=f(x)andy=f(c)(where c∈(a,b)) is minimum when c=a+b2.
Proof : A=∫ca(f(c)−f(x))dx+∫bc(f(c))dx
=f(c)(c−a)−∫ca(f(x))dx+∫ba(f(x))dx−f(c)(b−c)
⇒ A=[2c−(a+b)]f(c)+∫bc(f(x))dx−∫ca(f(x))dx
Differentiating w.r.t. c, we get
dAdc=[2c−(a+b)]f'(c)+2f(c)+0−f(c)−(f(c)−0)
For maxima and minima , dAdc=0
⇒ f'(c)[2c−(a+b)]=0(asf'(c)≠0)
Hence, c=a+b2
Also for c<a+b2,dAdc<0 and for c>a+b2,dAdc>0
Hence, A is minimum when c=a+b2.
If the area enclosed by f(x)=sinx+cosx,y=a between two consecutive points of extremum is minimum, then the value of a is
View SolutionConsider f(x)= minimum (x+2,√4−x),∀x≤4. If the area bounded by y=f(x) and the x - axis is 22k square units, then the value of k is
View SolutionThe area bounded by the graph of y=f(x),f(x)>0 on [0,a] and x-axis is a22+a2sina+π2cosa then find the value of f(π2).
View SolutionLet f(x)=x−x2 and g(x)=ax. If the area bounded by f(x) and g(x) is equal to the area bounded by the curves x=3y−y2 and x+y=3, then find the value of |[a]|:
[Note: denotes the greatest integer less than or equal to k.]
View Solution
