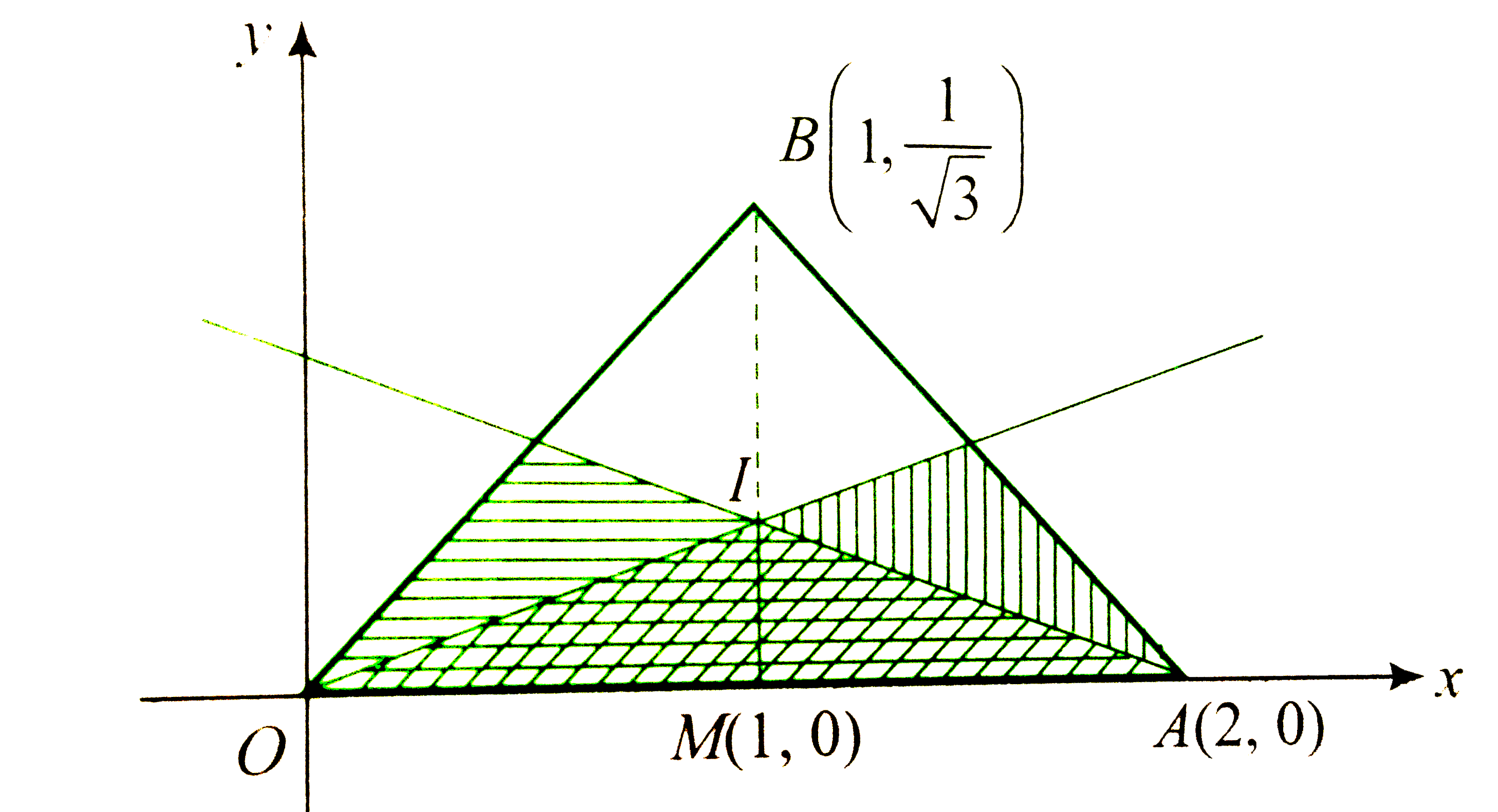
Let O(0,0),A(2,0),andB(11√3) be the vertices of a triangle. Let R be the region consisting of all those points P inside OAB which satisfy d(P,OA)≤min[d(p,OB),d(P,AB)] , where d denotes the distance from the point to the corresponding line. Sketch the region R and find its area.
d(P,OA)≤ min [d(P,OB),d(P,AB)]
⇒ d(P,OA)≤d(P,OB)andd(P,OA)≤d(P,AB)
When d(P,OA)=d(P,OB),P is equidistant from OA and OB, or
P lies on the angular bisector of lines OA and OB.
Hence when d(P,OA)≤d(P,OB), point P is nearer to OA than to
OB, i.e., lies on or below the bisector of OA and OB.
Similarly, when d(P,OA)≤d(P,AB), P is nearer to OA then to OB, i.e., lies on or below the bisector of OA and AB.
∴ Required area = Area of ΔOIA.
Now, tan ∠BOA=1/√31=1√3
or ∠BOA=30∘⇒∠IOA=15∘
⇒ IM=tan15∘=2−√3.
Hence, Area of ΔOIA=12OA×IM=12×2×(2−√3)
2−√3 sq. units.
Topper's Solved these Questions
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Solved Examples
10 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Concept Application Exercise 9.1
9 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
Similar Questions
Consider the traingle having vertices O(0,0),A(2,0), and B(1,√3). Also b≤min{a1,a2,a3....an} means b≤a1 when a1 is least, b≤a2 when a2 is least, and so on. Form this, we can say b≤a1,b≤a2,.....b≤an.
Let R be the region consisting of all those points P inside ΔOAB which satisfy d(P,OA)≤min[d(P,OB),d(P,AB)], where d denotes the distance from the point to the corresponding line. then the area of the region R is
View SolutionConsider a ΔOAB formed by the point O(0,0),A(2,0),B(1,√3).P(x,y) is an arbitrary interior point of triangle moving in such a way that d(P,OA)+d(P,AB)+d(P,OB)=√3, where d(P,OA),d(P,AB),d(P,OB) represent the distance of P from the sides OA,AB and OB respectively
Area of region reperesenting all possible position of point P is equal to
View SolutionA(3,4),B(0,0)andc(3,0) are vertices of ΔABC. If 'P' is the point inside the ΔABC, such that d(P,BC)≤ min. {d(P,AB),d(P,AC)}. Then the maximum of d(P,BC) is.(where d(P,BC) represent distance between PandBC).
View SolutionThe vertices of a triangle are O(0,0), A(a,0)and B(0,b) . Write the coordinates of its circumcentre.
View SolutionLet O(0,0),P(3,4), and Q(6,0) be the vertices of triangle OPQ . The point R inside the triangle OPQ is such that the triangles OPR,PQR,OQR are of equal area. The coordinates of R are a. (43,3) b. (3,23) c. (3,43) d. (43,23)
View SolutionLet O(0,0),P(3,4), and Q(6,0) be the vertices of triangle OPQ . The point R inside the triangle OPQ is such that the triangles OPR,PQR,OQR are of equal area. The coordinates of R are (43,3) (b) (3,23) (3,43) (d) (43,23)
View SolutionLet AP and BQ be two vertical poles at points A and B, respectively. If AP=16m,BQ=22mandAB=20m, then find the distance of a point R on AB from the point A such that RP2+RQ2is minimum.
View SolutionLet L1=0andL2=0 be two fixed lines. A variable line is drawn through the origin to cut the two lines at R and S.P. is a point on the line AB such that (m+n)OP=mOR+nOS. Show that the locus of P is a straight line passing through the point of intersection of the given lines R,S,R are on the same side of O).
View SolutionLet P(x) denote the probability of the occurrence of event x. Plot all those point (x,y)=(P(A),P(B)) in a plane which satisfies the conditions, P(A∪B)≥3/4and1/8≤P(A∩B)≤3/8
View SolutionLet O≡(0,0),A≡(0,4),B≡(6,0). Let P be a moving point such that the area of triangle POA is two times the area of triangle POB . The locus of P will be a straight line whose equation can be
View Solution
