Question

The area of the region described by $A=\{(x,y):x^2+y^2\le 1\text{and}{y}^2\le 1-x\}$ is

Options

A. `(pi)/(2)+(4)/(3)`
B. `(pi)/(2)-(4)/(3)`
C. `(pi)/(2)-(2)/(3)`
D. `(pi)/(2)+(2)/(3)`

Answer

D

Explanation

`x^(2)+y^(2)le1" represents the rgeion inside the circle "x^(2)+y^(2)=1.`

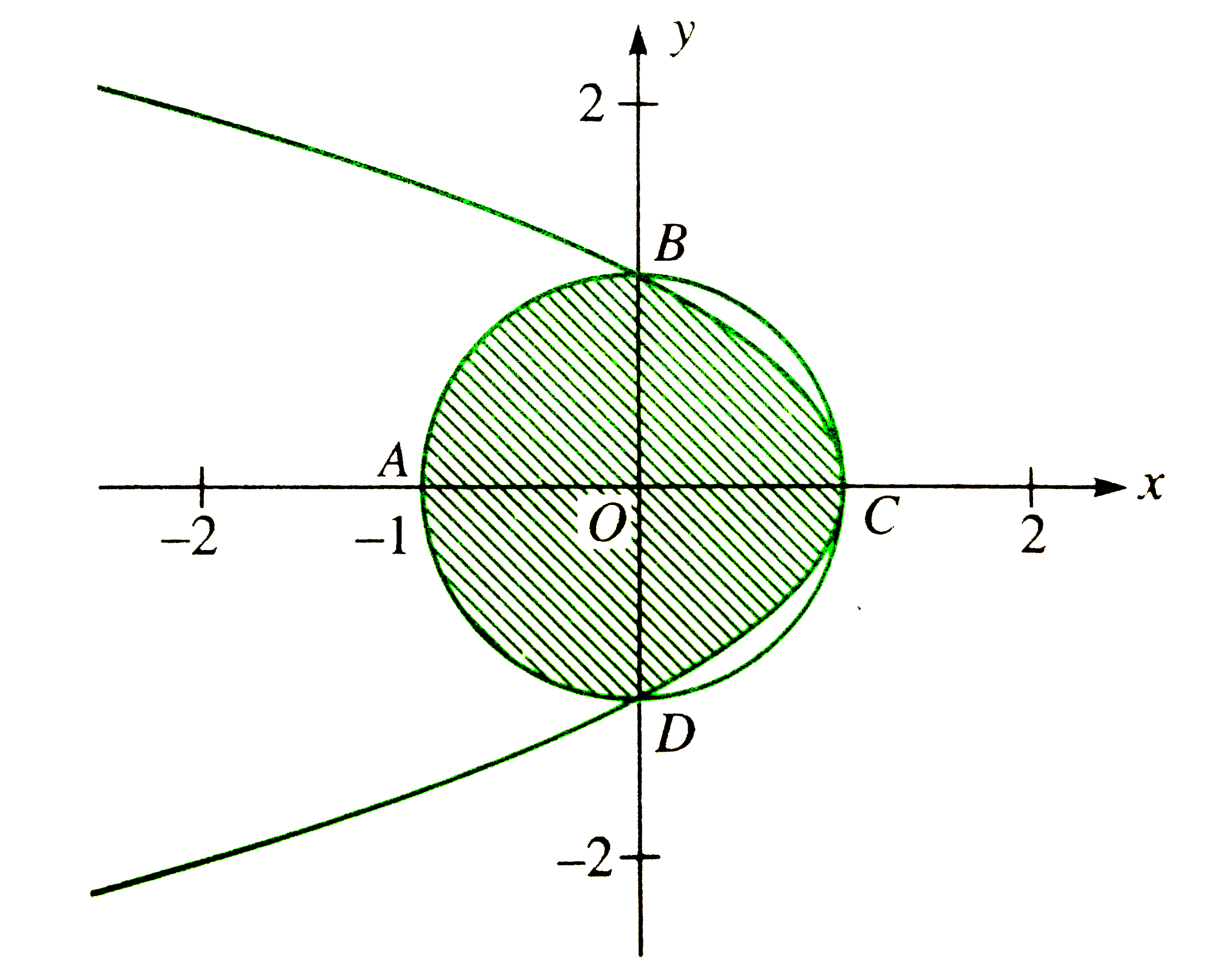
`y^(2)le1-x`, represents the region inside parabola `y^(2)=1-x` towards focus.
The common region is as shown in the figure.
The area of shaded region
= Area of semicircle ADOBA+ Area of region ODCBO
`=(pi)/(2)+2overset(1)underset(0)int(1-y^(2))dy`
`=(pi)/(2)+2[y-(y^(3))/(3)]_(0)^(1)`
`=(pi)/(2)+2[1-(1)/(3)]`
`=(pi)/(2)+(2)/(3)`