If (a,b) be an end of a diagonal of a square and the other diagonals has the equation x−y=a then another vertex of the square can be
(a−b,a)
(a,0)
(0,−a)
(a+b,b)
The correct Answer is:B, D
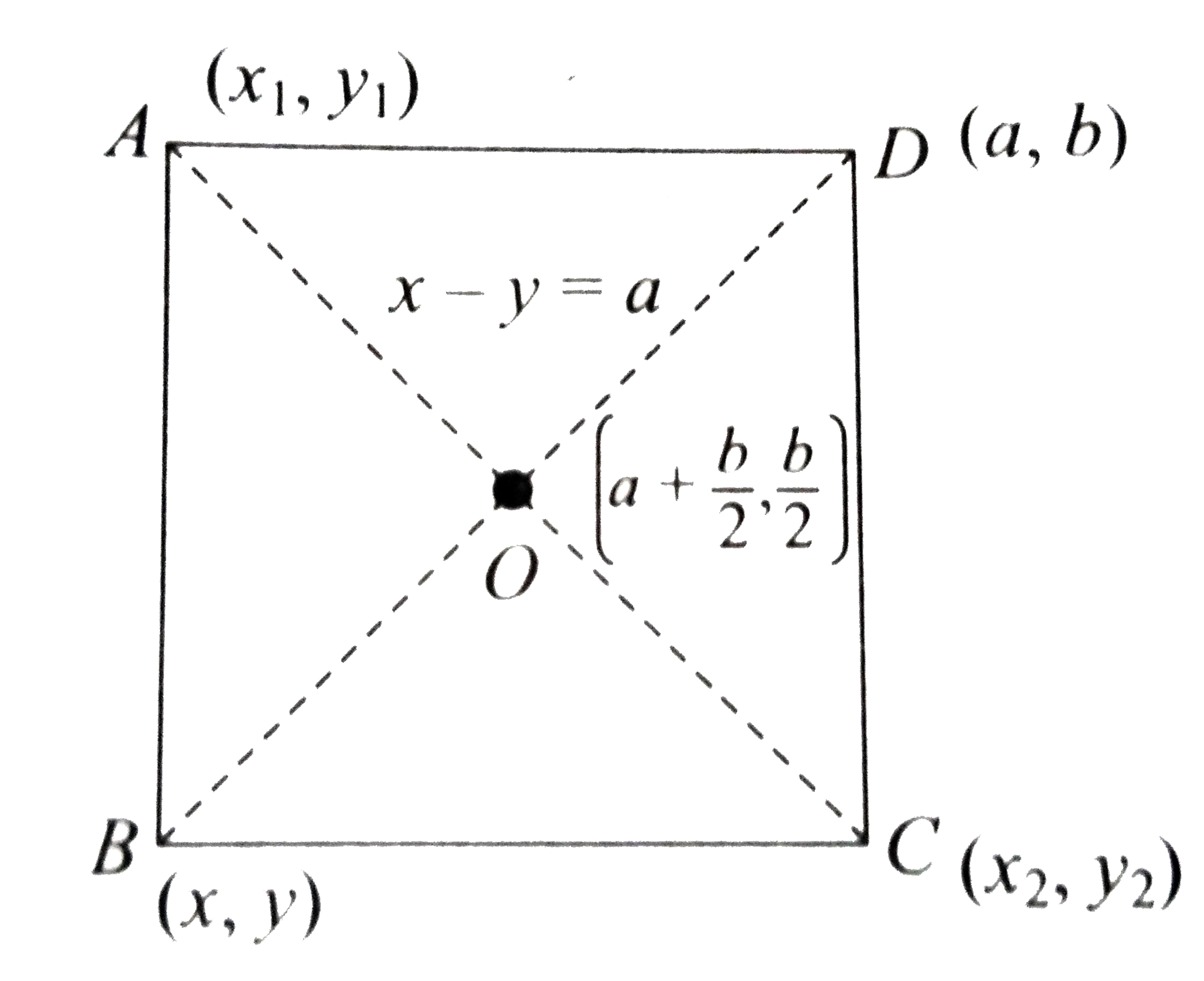
Diagonal AC is x−y=a
∴ Slope BD=−1
Also BD passes through (a,b)
∴ Equation of BD is x+y=a+b
Solving, we get point O≡(a+b2,b2)
∴ point B≡(a+b,0)
mAC=1=tanθ
OA=OD=b√2
Using parametric form of straight line points A and C are given by
(a+b2±b√2cos45∘,b2±b√2sin45∘)
or A(a,0) and C(a+b,b)
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If the end points of the diagonal of a square are (-2,3,1) and (-3,5,2) , then the length of the side of the square is
A√2 unitsB√3 unitsC√6 unitsD2√3 units
The ends of a diagonal of a square have co-ordinates (−2,p)and(p,2). Find p, if the area of the square is 40 sq. units.
View SolutionA square has one vertex at the vertex of the parabola y2=4ax and the diagonal through the vertex lies along the axis of the parabola. If the ends of the other diagonal lie on the parabola, the coordinates of the vertices of the square are (a)(4a,4a) (b) (4a,−4a) (c)(0,0) (d) (8a,0)
View SolutionWhat is the area of a square with diagonal of 6?
View SolutionOne diagonal of a square is the portion of the line 7x+5y=35 intercepted by the axes. Obtain the extremities of the other diagonal.
View SolutionThe co-ordinates of the vertex A of a square ABCD are (1, 2) and the equation of the diagonal BD is x+2y=10. Find the equation of the other diagonal and the co-ordinates of the centre of the square.
View SolutionIf one of the sides of a square is 3x-4y-12 = 0 and the center is (0,0), then find the equations of the diagonals of the square.
View SolutionIf one of the sides of a square is 3x−4y−12=0 and the center is (0,0) , then find the equations of the diagonals of the square.
View Solution

