The equation of the diagonals of a rectangle are y+8x−17=0 and y−8x+7=0. If the area of the rectangle is 8squnits then find the sides of the rectangle
x=1
x+y=1
y=9
x−2y=3
The correct Answer is:A, C
To solve the problem, we need to find the sides of a rectangle given the equations of its diagonals and the area. Let's go through the solution step by step.
Step 1: Find the point of intersection of the diagonals
The equations of the diagonals are:
1. y+8x−17=0
2. y−8x+7=0
To find the point of intersection, we can solve these equations simultaneously.
From the first equation:
y=17−8x
Substituting this into the second equation:
17−8x−8x+7=0
24−16x=0
16x=24⟹x=2416=32
Now substituting x=32 back into the first equation to find y:
y=17−8(32)=17−12=5
Thus, the point of intersection P is (32,5).
Step 2: Determine the slopes of the diagonals
The slopes of the lines can be found by rearranging the equations into slope-intercept form y=mx+c.
1. For y+8x−17=0:
y=−8x+17(slope m1=−8)
2. For y−8x+7=0:
y=8x−7(slope m2=8)
Step 3: Calculate the angle between the diagonals
The angle θ between the two lines can be calculated using the formula:
tanθ=∣∣∣m1−m21+m1m2∣∣∣
Substituting the slopes:
tanθ=∣∣∣−8−81+(−8)(8)∣∣∣=∣∣∣−161−64∣∣∣=∣∣∣−16−63∣∣∣=1663
Step 4: Relate the sides of the rectangle to the area
Let the lengths of the sides of the rectangle be a and b. The area A of the rectangle is given by:
A=a⋅b=8 square units
Step 5: Use the relationship with the angle
From the geometry of the rectangle, we know:
tanθ=a/2b/2=ab
Thus,
ab=1663⟹a=1663b
Step 6: Substitute into the area equation
Substituting a into the area equation:
(1663b)b=8
1663b2=8
b2=8⋅6316=50416=632
b=√632=√1262
Now substituting back to find a:
a=1663b=1663⋅√1262=8√12663
Final Result
Thus, the sides of the rectangle are:
a=8√12663,b=√1262
1. y+8x−17=0
2. y−8x+7=0
y=17−8x
17−8x−8x+7=0
24−16x=0
16x=24⟹x=2416=32
y=17−8(32)=17−12=5
y=−8x+17(slope m1=−8)
y=8x−7(slope m2=8)
tanθ=∣∣∣m1−m21+m1m2∣∣∣
Substituting the slopes:
tanθ=∣∣∣−8−81+(−8)(8)∣∣∣=∣∣∣−161−64∣∣∣=∣∣∣−16−63∣∣∣=1663
A=a⋅b=8 square units
tanθ=a/2b/2=ab
Thus,
ab=1663⟹a=1663b
(1663b)b=8
1663b2=8
b2=8⋅6316=50416=632
b=√632=√1262
a=1663b=1663⋅√1262=8√12663
a=8√12663,b=√1262
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
AC, a diagnonal of the rectange ABCD , measure 5 units. The area of the rectangle is 12 sq. units. What is the perimeter of the rectangle?
A7B14C17D20
find the length of the diagonal of a rectangle whose sides are 8 m and 6m.
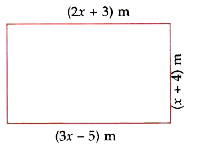
View SolutionThe measurements of the sides of a rectangle are given. Find
(i) the value of x.
(ii) the area of the rectangle
(iii) the perimeter of the rectangle .
 View Solution
View SolutionIf a rectangle has breadth 11 m and area 264 sq. m, what is the length of the rectangle? Also, find the perimeter of the rectangle.
View SolutionThe area of a rectangle is 194.04 sq. cm. If the length of the rectangle is 14.7cm, find its breadth.
View SolutionFind the equations of the diagonals of a rectangle whose sides are x + 1 = 0, x - 4 = 0, y + 1 = 0 and y - 2 = 0.
View SolutionThe area of a square and a rectangle are equal.If the side of the square is 40 cm and the breadth of the rectangle is 25 cm,find the length of the rectangle. Also,find the perimeter of the rectangle.
View SolutionThe equation of one side of a rectangle is 3x−4y−10=0 and the coordinates of two of its vertices are (−2,1)and(2,4). Then, the area of the rectangle is
View Solution

