Question

The maximum distance of the centre of the ellipse $\frac{x^2}{16}+\frac{y^2}{9}=1$ from the chord of contact of mutually perpendicular tangents of the ellipse is

Options

A. `(144)/(5)`
B. `(9)/(5)`
C. `(16)/(5)`
D. `(8)/(5)`

Answer

C

Explanation

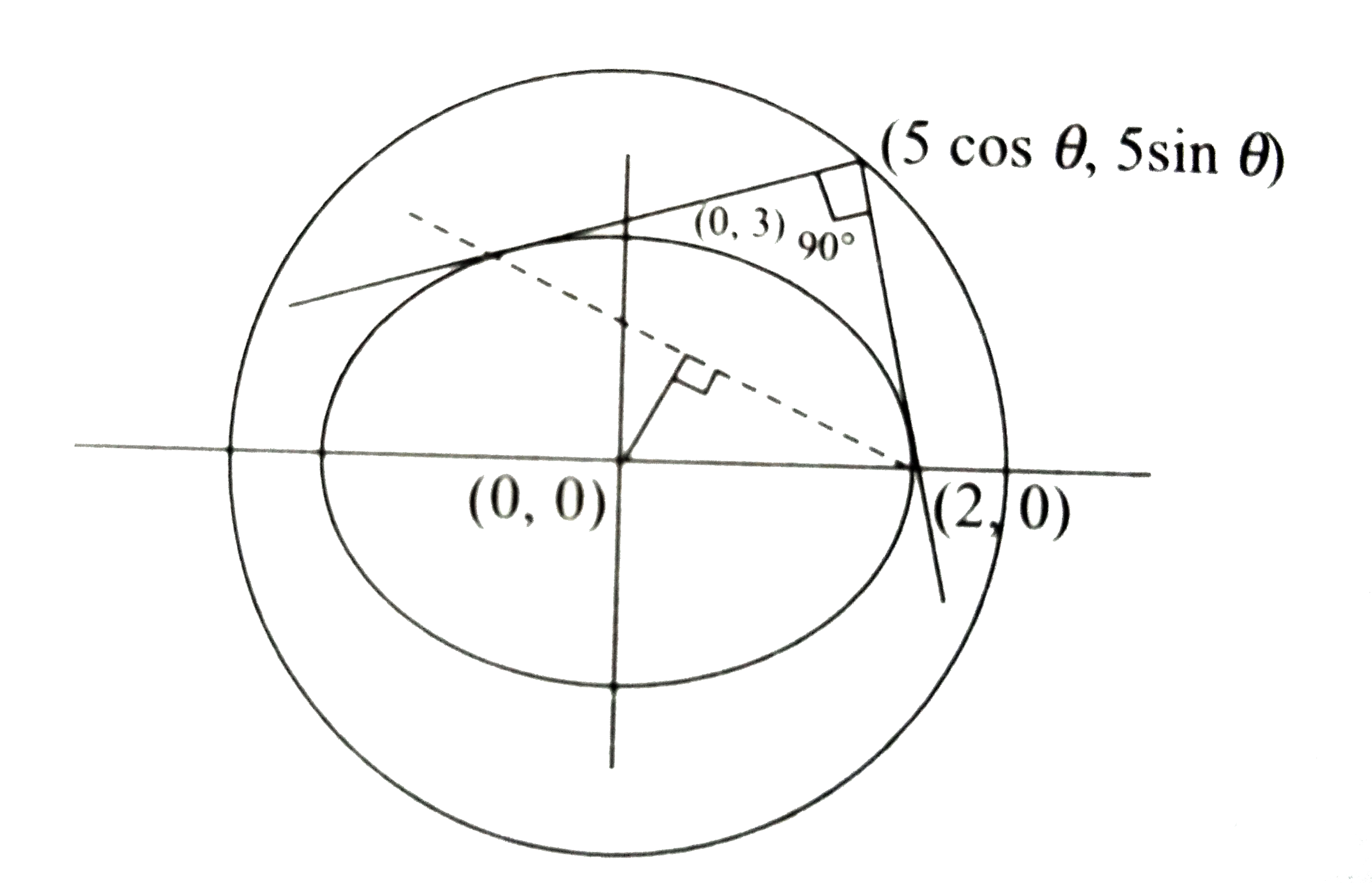
Perpendicular tangents meet on director circle `x^(2) + y^(2) = 25`, Any point on this circle is `P(5 cos theta, 5 sin theta)`
Equation of chord of contact of ellipse w.r.t this point is
`(5 cos theta x)/(16) + (5 sin theta y)/(9) =1`
Distance from center `= (1)/(sqrt((25)/(256)cos^(2)theta+(25)/(81)sin^(2)theta))`
For maximum value `cos theta =1` and `sin theta = 0`
Maximum distance `= (16)/(5)`