Find the equation of the circle having center at (2,3) and which touches $x + y = 1$ .

Video Solution

Text Solution

Verified by Experts

The centre of the circle is $C (2, 3)$ .

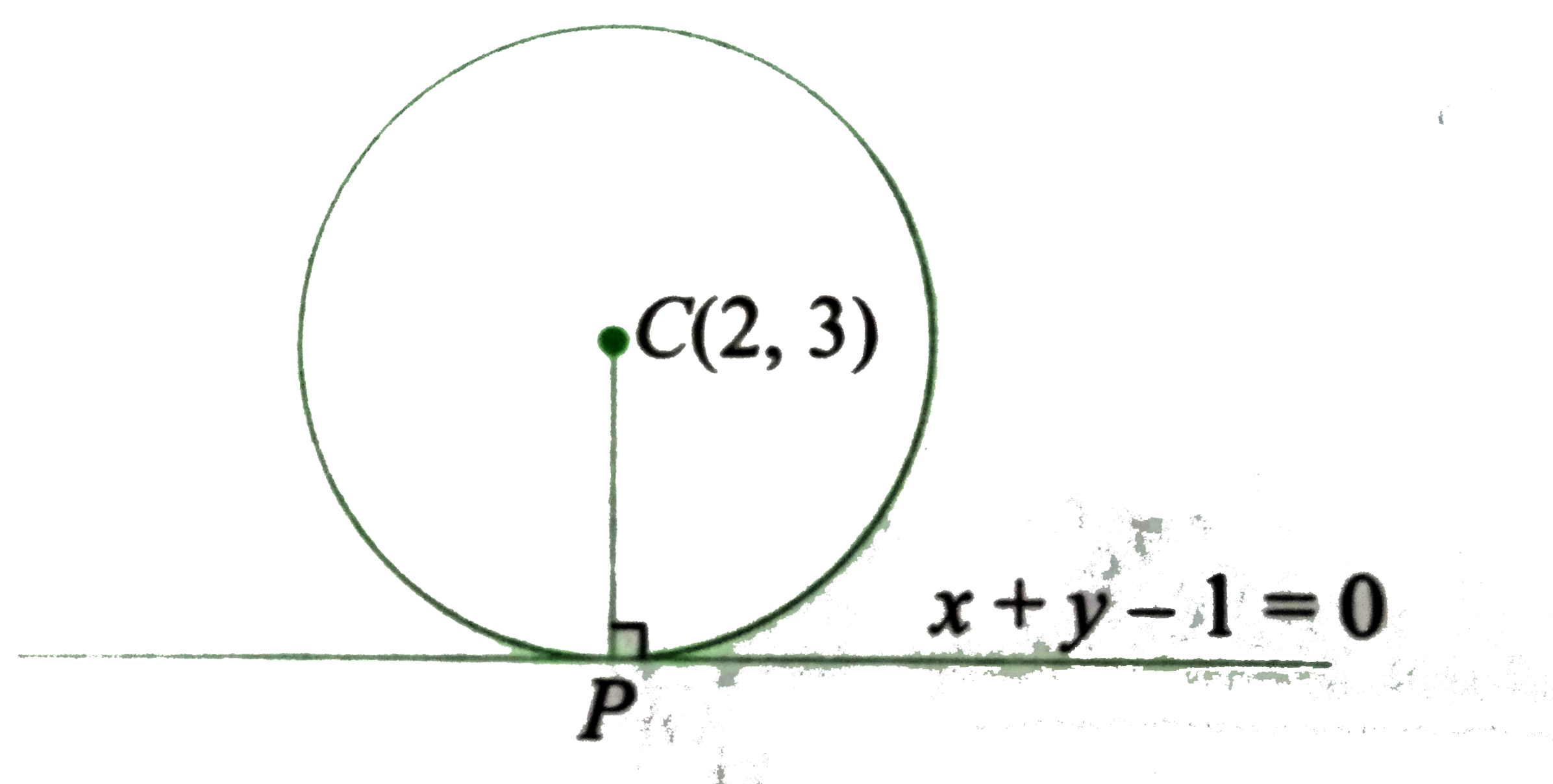
Also, line $x + y - 1 = 0$ is tangent to the circle.
Hence, the radius of the circle is the perpendicular distance of centre from the tangent.
Therefore, radius $r = C P = \frac{| 2 + 3 - 1 |}{\sqrt{1^{2} + 1^{2}}} = 2 \sqrt{2}$
Hence, the equation of circle is ${(x - 2)}^{2} + {(y - 3)}^{2} = 8$

Updated on:21/07/2023

|

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

The equation of the circle whose center is (3,-2) and which touches the line $3 x - 4 y + 13 = 0$ is
AA. $x^{2} + y^{2} + 6 x - 4 y - 23 = 0$
BB. $x^{2} + y^{2} - 6 x - 4 y - 23 = 0$
CC. $x^{2} + y^{2} - 6 x + 4 y - 23 = 0$
DD. $x^{2} + y^{2} + 6 x + 4 y + 23 = 0$

CENGAGE ENGLISH-CIRCLE -MATRIX MATCH TYPE

Home
Ask Doubt
Profile