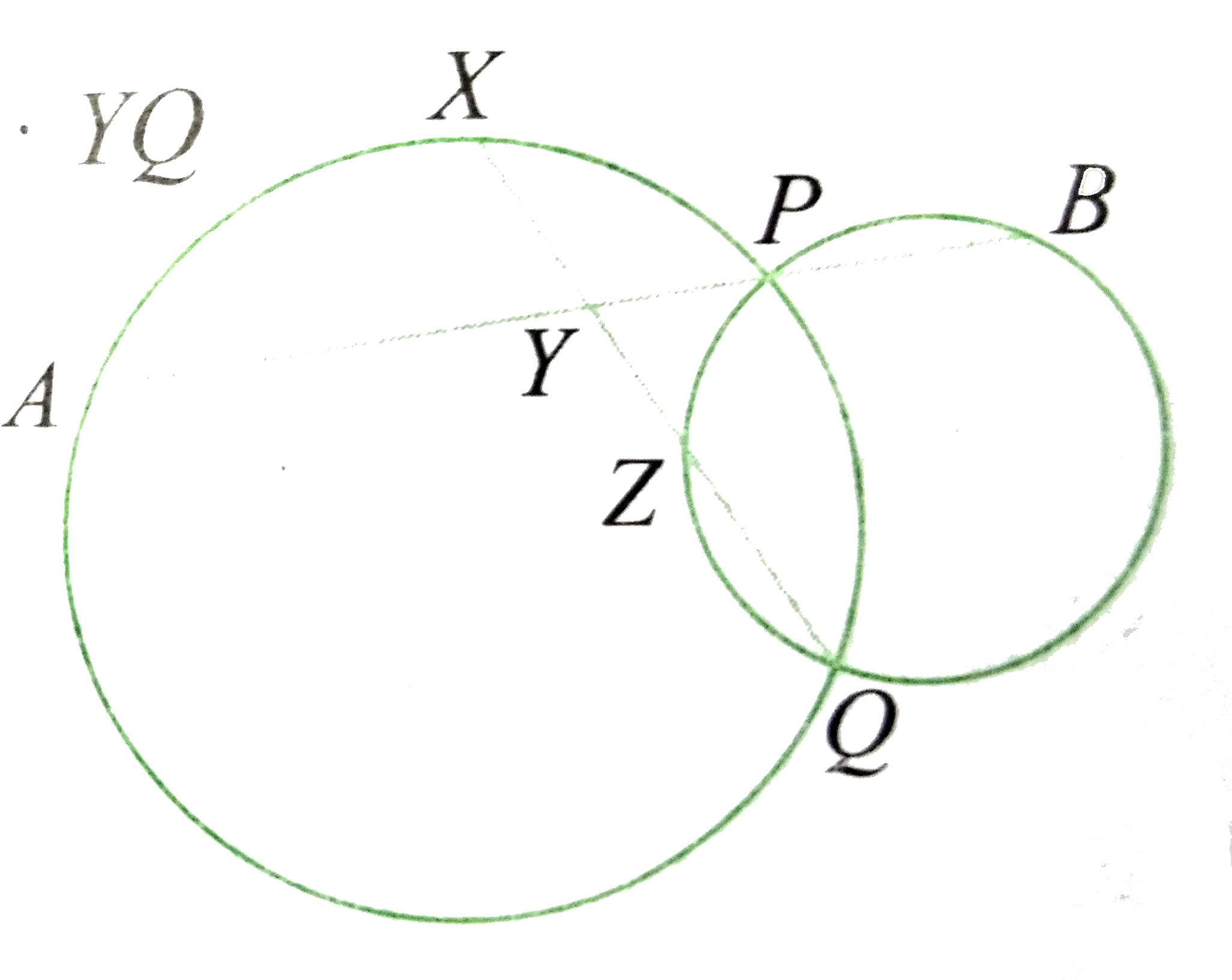
Two circles C1andC2 intersect at two distinct points PandQ in a line passing through P meets circles C1andC2 at AandB , respectively. Let Y be the midpoint of AB,andQY meets circles C1andC2 at XandZ , respectively. Then prove that Y is the midpoint of XZ.
From the figure, YP.YB=YZ.YQ
and YA.YP=YX.YQ
But YA=YB
Hence, XY=YZ
So, Y is midpoint of XZ.
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Examples13videos
CIRCLE
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.11videos
CIRCLE
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix4videos
BINOMIAL THEOREM
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
Similar Questions
Two circles C1 and C2 intersect at two distinct points PandQ in a line passing through P meets circles C1andC2 at AandB , respectively. Let Y be the midpoint of AB and QY meets circles C1 andC2 at Xa n dZ respectively. Then prove that Y is the midpoint of XZ
View SolutionConsider two lines L1andL2 given by a1x+b1y+c1=0anda2x+b2y+c2=0respectivelywherec1andc2≠0, intersecting at point P.A line L3 is drawn through the origin meeting the lines L1andL2 at AandB, respectively, such that PA=PB . Similarly, one more line L4 is drawn through the origin meeting the lines L1andL2 at A1andB2, respectively, such that PA1=PB1. Obtain the combined equation of lines L3andL4.
View SolutionIn an isosceles triangle ABC with AB=AC, a circle passing through B and C intersects the sides ABandAC atDandE respectively. Prove that DE∣∣BC.
View SolutionA line passing through the origin O(0,0) intersects two concentric circles of radii aandb at PandQ, If the lines parallel to the X-and Y-axes through QandP, respectively, meet at point R, then find the locus of R.
View SolutionIf a,b,c are in G.P. and x,y are the arithmetic means of a,bandb,c respectively, then prove that ax+cy=2and1x+1y=2b
View SolutionTwo circles with centres AandB of radii 3cmand4cm respectively intersect at two points CandD such that ACandBC are tangents to the two circles. Find the length of the common chord CD.
View SolutionA point P moves on a plane xa+yb+zc=1. A plane through P and perpendicular to OP meets the coordinate axes at A,BandC. If the planes through A,BandC parallel to the planes x=0,y=0andz=0, respectively, intersect at Q, find the locus of Q.
View SolutionA point P moves on a plane xa+yb+zc=1. A plane through P and perpendicular to OP meets the coordinate axes at A,BandC. If the planes through A,BandC parallel to the planes x=0,y=0andz=0, respectively, intersect at Q, find the locus of Q.
View SolutionIn Figure, PandQ are the midpoints of the sides CAandCB respectively of ABC right angled at C. Prove that 4(AQ2+BP2)=5AB2 .
View SolutionTwo circles C1andC2 both pass through the points A(1,2)andE(2,1) and touch the line 4x−2y=9 at BandD, respectively. The possible coordinates of a point C, such that the quadrilateral ABCD is a parallelogram, are (a,b). Then the value of |ab| is_________
View Solution

