The area of the triangle formed by the positive x-axis with the normal and the tangent to the circle x2+y2=4 at (1,√3) is
The correct Answer is:2√3sq. unit
Equation of tangent to circle x2+y2=4 at point P(1,√3) is 1.x+√3.y=4,i.e.,x+√3y=4.
It meets x-axis at A(4,0) .
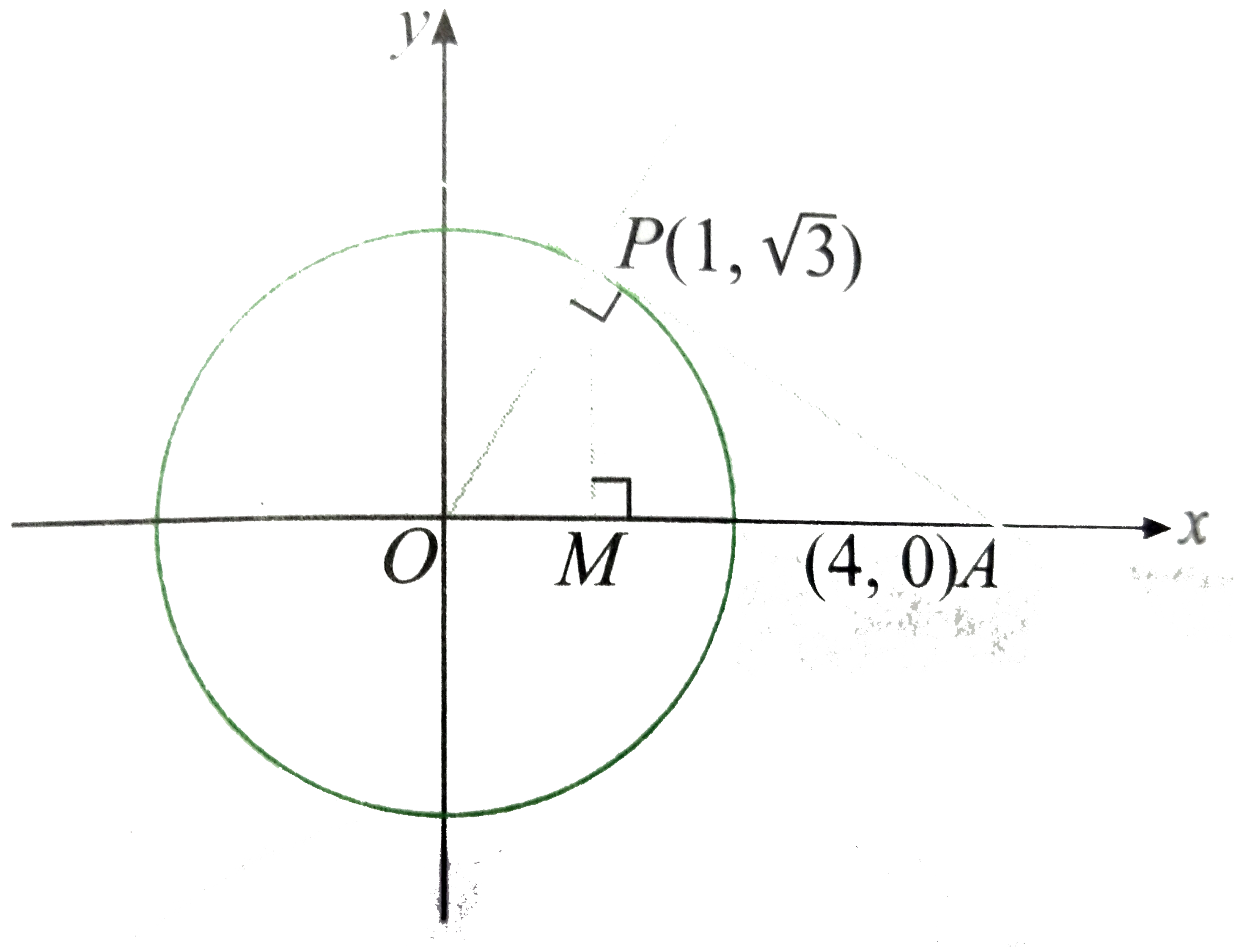
∴ Area of triangle OAP=12OA×PM
=124×√3=2√3
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.95videos
CIRCLE
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.105videos
CIRCLE
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.75videos
CIRCLE
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix4videos
BINOMIAL THEOREM
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
Similar Questions
The area of the triangle formed by the positive x− axis and the normal and tangent to the circle x2+y2=4 at (1,√3) is (a)2√3sq.units (b) 3√2sq.units (c)√6sq.units (d) none of these
View SolutionUsing integration, find the area of the triangle formed by positive x-axis and tangent and normal to the circle x2+y2=4 at (1,√3).
View SolutionUsing integration, find the area of the triangle formed by negative x-axis and tangent and normal to the circle x2+y2=9 at (−1,2√2).
View SolutionThe area of the triangle formed with coordinate axes and the tangent at (x1,y1) on the circle x2+y2=a2 is
View SolutionThe area of the triangle formed by the tangent at the point (a, b) to the circle x2+y2=r2 and the coordinate axes, is
View SolutionFind the area of the triangle formed by the line x+y=3 and the angle bisectors of the pair of lines x2−y2+4y−4=0
View SolutionThe area (in sq units) of the triangle formed by the tangent, normal at (1,√3) to the circle x2+y2=4 and the X-axis, is
View SolutionFind the area of the triangle formed by the lines y=x,y=2x,y=3x+4
View SolutionFind the area of the triangle formed by the lines y=x,y=2x,y=3x+4
View SolutionThe area of triangle formed by the lines x−y=0,x+y=0 and any tangent to the hyperbola x2−y2=16 is equal to
View Solution
