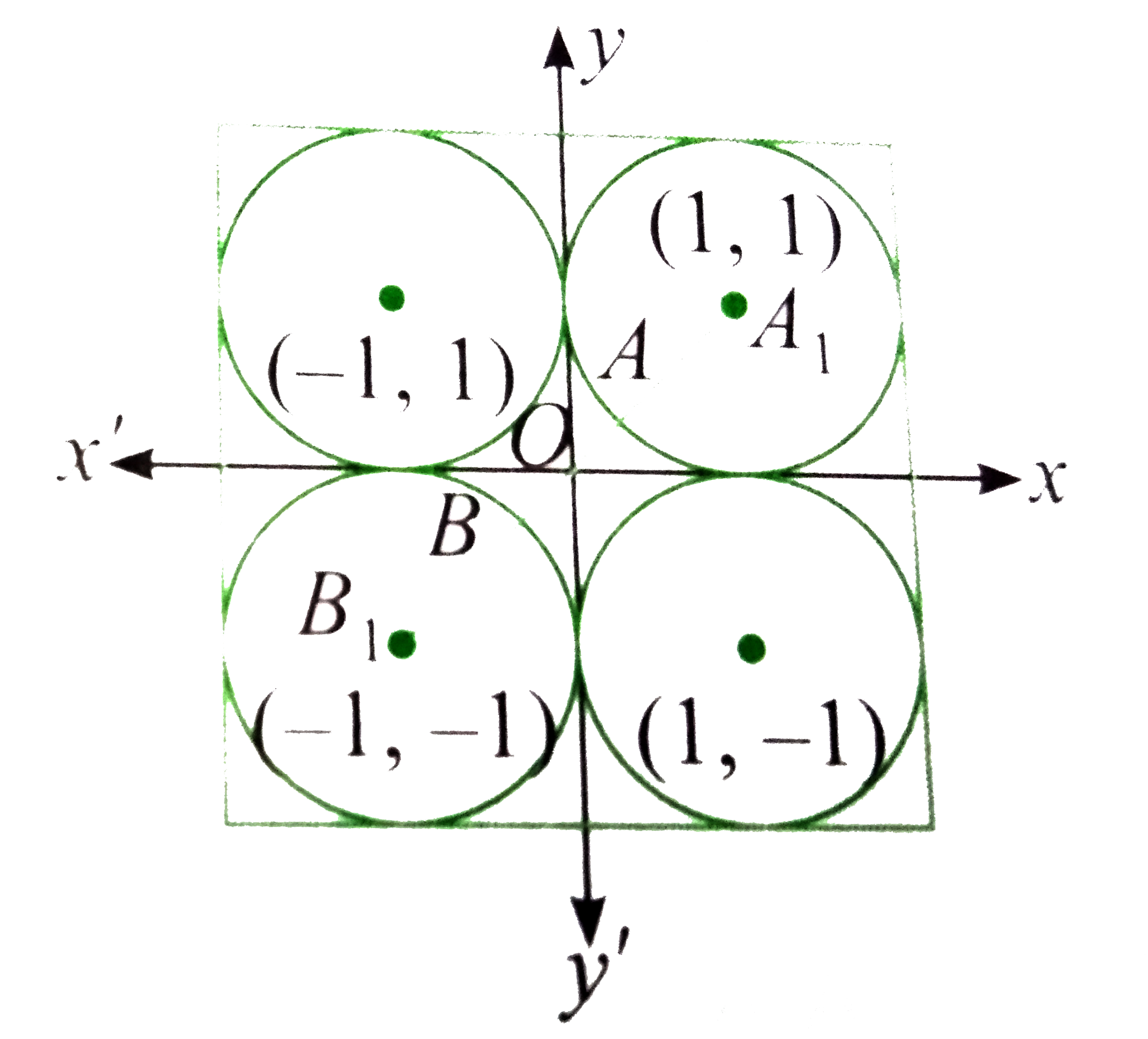
Consider four circles (x±1)2+(y±1)2=1 . Find the equation of the smaller circle touching these four circles.
The correct Answer is:x2+y2=3−2√2
A1B1=√4+4=2√2
∴AB=2√2−2=2(√2−1)
Thus, the equation of the required circle isx2+y2=(√2−1)2=3−2√2
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.134videos
CIRCLE
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.144videos
CIRCLE
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.114videos
CIRCLE
- BOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix4videos
BINOMIAL THEOREM
- BOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type8videos
CIRCLES
Similar Questions
Find the equation of the family of circles touching the lines x2−y2+2y−1=0.
View SolutionFind the equation of the circle which touches x-axis and whose centre is (1,2).
View SolutionThe equation of a circle is x2+y2=4. Find the center of the smallest circle touching the circle and the line x+y=5√2
View SolutionThe equation of a circle is x2+y2=4. Find the center of the smallest circle touching the circle and the line x+y=5√2
View SolutionFind the equation of the circle which touches the x-axis and whose center is (1, 2).
View SolutionFind the equation of the circle which touches the x-axis and whose center is (1, 2).
View SolutionFind the equation of the circle which touches the x-axis and whose center is (1, 2).
View SolutionFind the equation of a circle with center (4, 3) touching the circle x2+y2=1
View SolutionThe equation of four circles are (x±a)2+(y±a2=a2 . The radius of a circle touching all the four circles is (√2+2)a (b) 2√2a (√2+1)a (d) (2+√2)a
View SolutionFind the equation of a circle with center (4, 3) touching the line x+y=1
View Solution

