Question

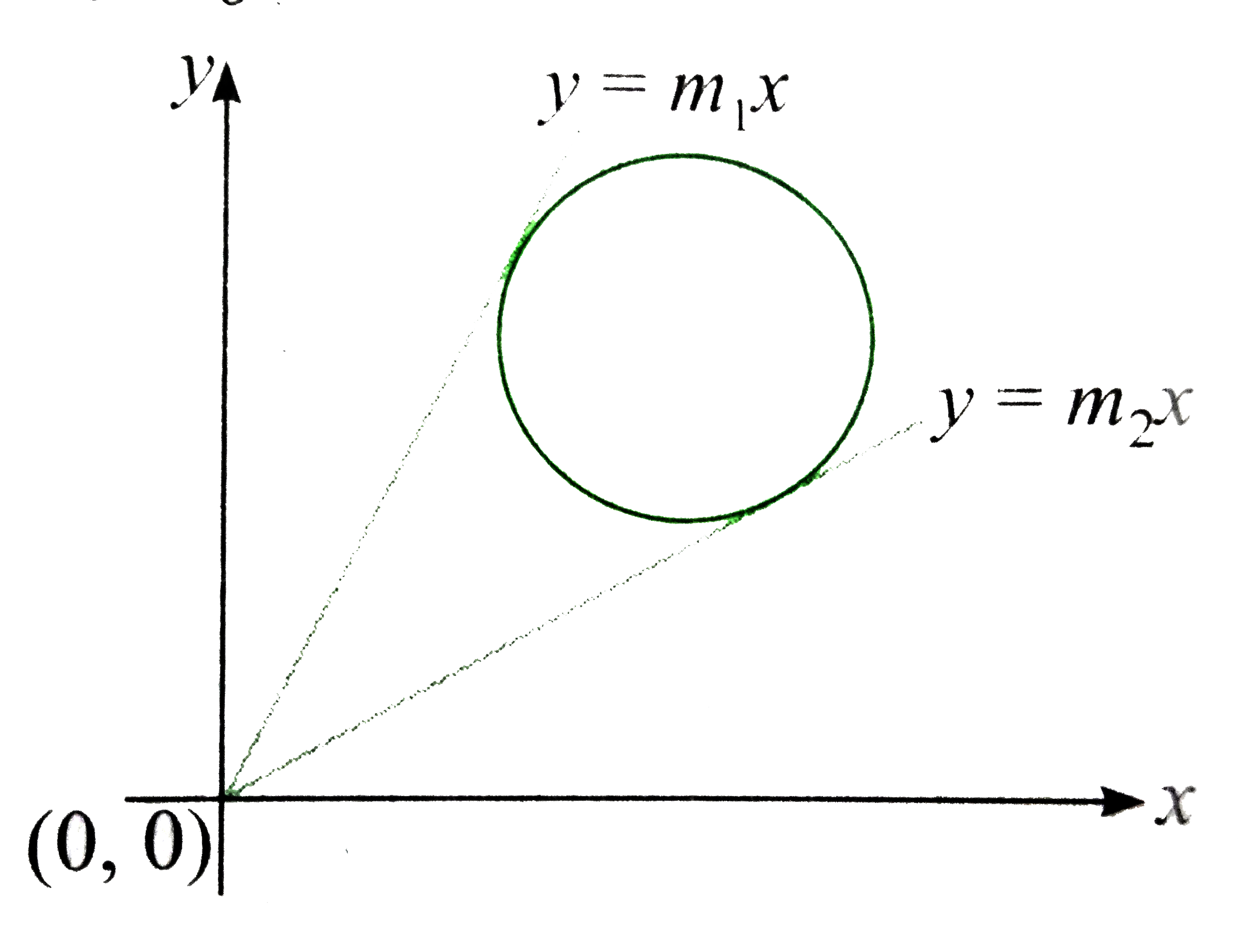
Consider a circle ${\displaystyle x^2+y^2+ax+by+c=0}$
lying completely in the first quadrant. If ${\displaystyle m_{1}and{m}_2}$
are the maximum and minimum values of ${\displaystyle \frac{y}{x}}$
for all ordered pairs ${\displaystyle (x,y)}$
on the circumference of the circle, then the value of ${\displaystyle (m_1+m_2)}$
is
${\displaystyle \frac{a^2-4c}{b^2-4c}}$

(b) ${\displaystyle \frac{2ab}{b^2-4c}}$

${\displaystyle \frac{2ab}{4c-b^2}}$

(d) ${\displaystyle \frac{2ab}{b^2-4ac}}$

Options

A. `(a^(2)-4c)/(b^(2)-4c)`
B. `(2ab)/(b^(2)-4c)`
C. `(2ab)/(4c-b^(2))`
D. `(2ab)/(b^(2)-4ac)`

Answer

3

Explanation

Substituting `y=mx` in the equation of circle, we get
`x^(2)+m^(2)x^(2)+ax+bmx+c=0`
`(y//x` denotes the slope of the tangent from the origin on the circles. )
Since the line is touching the circle, we must have discriminant.
`(a+bm)^(2)-4c(1+m^(2))=0` or `a^(2)+b^(2)m^(2)+2abm-4c-4cm^(2)=0`
or `m^(2)(b^(2)-4c)+2abm+a^(2)-4c=0`
This equation has two roots `m_(1)` and `m_(2)`. Therefore, `m_(1)+m_(2)= -(2ab)/(b^(2)-4c)=(2ab)/(4c-b^(2))`