The two circles which pass through $(0, a) a n d (0, - a)$ and touch the line $y = m x + c$ will intersect each other at right angle if $a^{2} = c^{2} (2 m + 1)$ $a^{2} = c^{2} (2 + m^{2})$ $c^{2} = a^{2} (2 + m^{2})$ (d) $c^{2} = a^{2} (2 m + 1)$

A

$a^{2} = c^{2} (2 m + 1)$

B

$a^{2} = c^{2} (2 + m^{2})$

C

$c^{2} = a^{2} (2 + m^{2})$

D

$c^{2} = a^{2} (2 m + 1)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:3

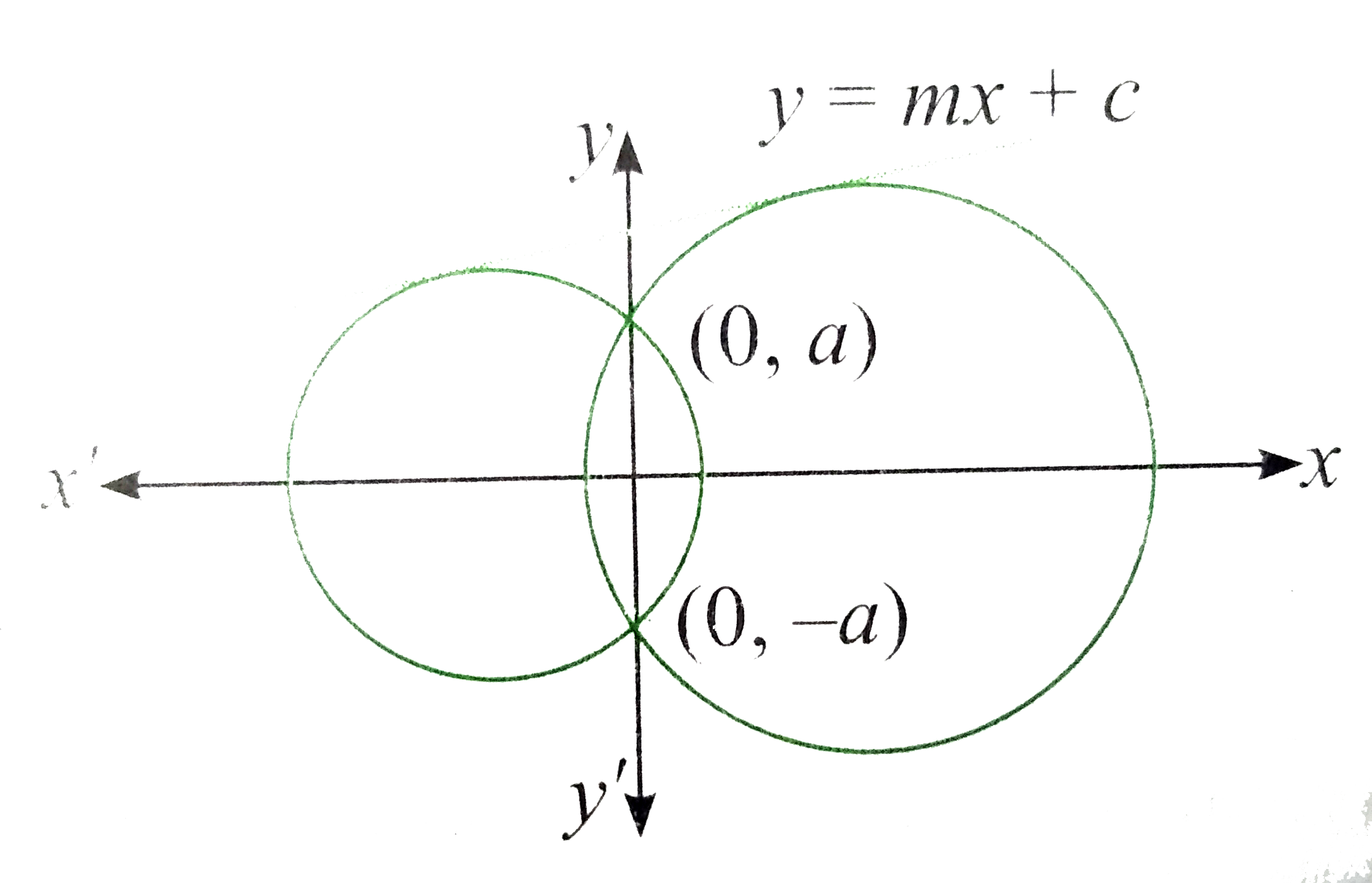
The equatio of the family of circles through (0,a) and (0,-a) is
$[x^{2} + (y - a) (y + a)] + λ x = 0, λ \in R$
or $x^{2} + y^{2} + λ x - a^{2} = 0$
Since circles touch line $y = m x + c$ ,
$\sqrt{{(\frac{λ}{2})}^{2} + a^{2}} = \frac{| (- m λ / 2) + c |}{\sqrt{1 + m^{2}}}$
or $(1 + m^{2}) [\frac{λ^{2}}{4} + a^{2}] = {(\frac{m λ}{2} - c)}^{2}$
or $(1 + m^{2}) [\frac{λ^{2}}{4} + a^{2}] = \frac{m^{2} λ^{2}}{4} - m c λ + c^{2}$
or $λ^{2} + 4 m c λ + 4 a^{2} (1 + m^{2}) - 4 c^{2} = 0$
$∴ λ_{1} λ_{2} = 4 [a (1 + m^{2}) - c^{2}]$
or $g_{1} g_{2} = [a^{2} (1 + m^{2}) - c^{2}]$
Now, $g_{1} g_{2} = f_{1} f_{2} = \frac{c_{1} + c_{2}}{2}$ (As circle cut orthogonally.)
$∴ a^{2} (1 + m^{2}) - c^{2} = - a^{2}$
Hence, $c^{2} = a^{2} (2 + m^{2})$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

CENGAGE ENGLISH-CIRCLE -Excercises (Single Correct Answer Type)

Home
Ask Doubt
Profile