Co-ordinates of the centre of a circle, whose radius is 2 unit and which touches the pair of lines $x^{2} - y^{2} - 2 x + 1 = 0$ is (are)

A

$(4, 0)$

B

$(1 + 2 \sqrt{2}, 0)$

C

$(4, 1)$

D

$(1, 2 \sqrt{2})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:2,4

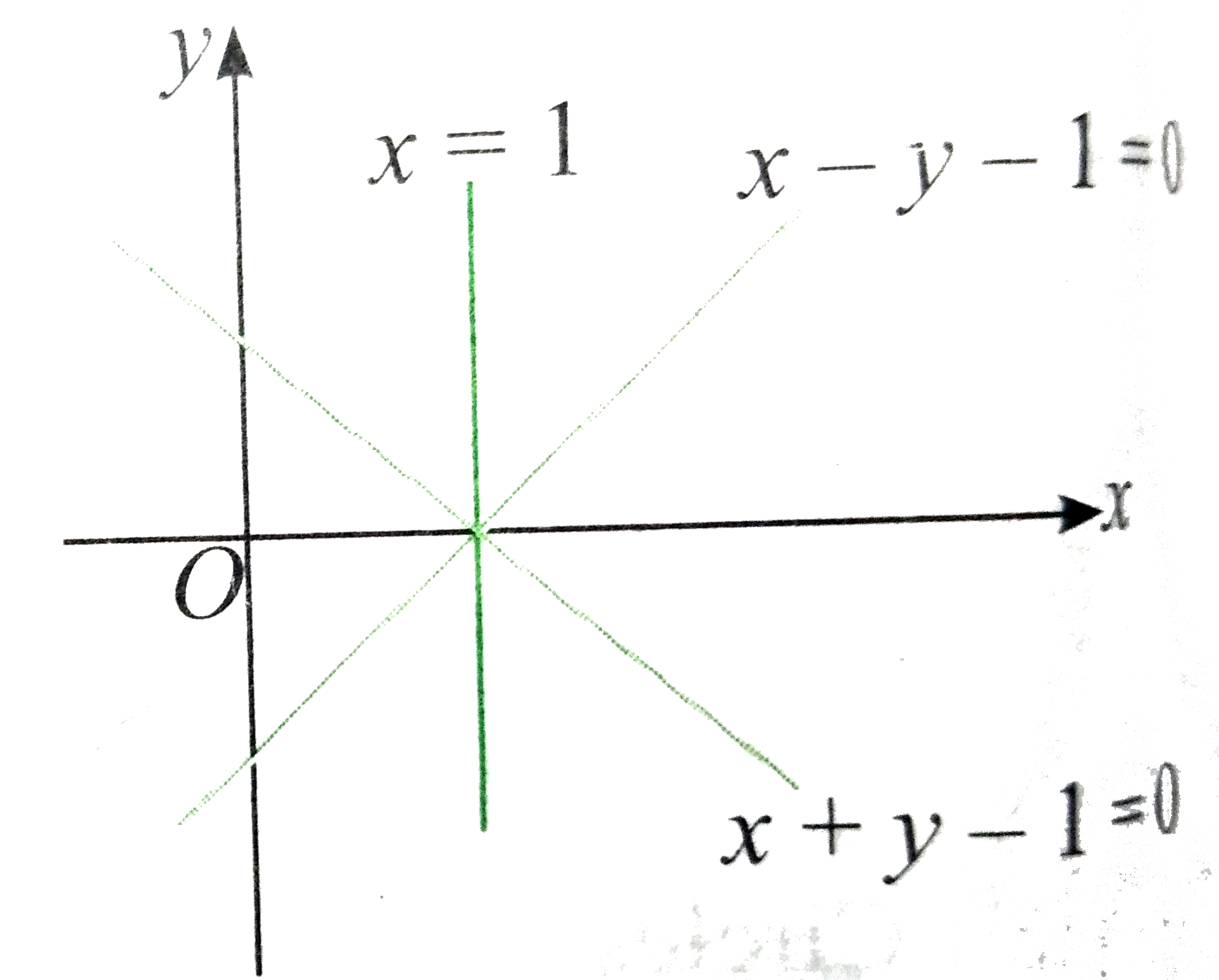
Line pair ${(x - 1)}^{2} - y^{2} = 0, i . e ., x + y - 1 = 0$ and $x - y - 1 = 0$ . Let the center be $(α, 0)$ . Then its distance from $x + y - 1 = 0$ is
$∣ ∣ ∣ \frac{α - 1}{\sqrt{2}} ∣ ∣ ∣ = 2$ (radius)
$i . e ., α = 1 \pm 2 \sqrt{2}$
So, the center may be $(1 + 2 \sqrt{2}, 0), (1 - 2 \sqrt{2}, 0)$ .
Now, let the center be $(1, β)$ . Then,
$∣ ∣ ∣ \frac{1 + β + 1}{\sqrt{2}} ∣ ∣ ∣ = 2$
or $β = \pm 2 \sqrt{2}$
So, the centre may be $(1, 2 \sqrt{2}), (1, - 2 \sqrt{2})$

Updated on:21/07/2023

|

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

The equation of the circle whose center is (3,-2) and which touches the line $3 x - 4 y + 13 = 0$ is
AA. $x^{2} + y^{2} + 6 x - 4 y - 23 = 0$
BB. $x^{2} + y^{2} - 6 x - 4 y - 23 = 0$
CC. $x^{2} + y^{2} - 6 x + 4 y - 23 = 0$
DD. $x^{2} + y^{2} + 6 x + 4 y + 23 = 0$

CENGAGE ENGLISH-CIRCLE -Multiple Correct Anser Type

Home
Ask Doubt
Profile