Each side of a square has length 4 units and its center is at (3,4). If one of the diagonals is parallel to the line $y = x$ , then anser the following questions.
The radius of the circle inscribed in the triangle formed by any three vertices is

A

$2 (\sqrt{2} - 1)$

B

$2 (\sqrt{2} + 1)$

C

$\sqrt{2} (\sqrt{2} - 1)$

D

none of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:1

It is given that one of the diagonals of the square is parallel to the line $y = x$
Also, the length of the diagonal of the square is $4 \sqrt{2}$
Hence, the equation of one of the diagonals is
$\frac{x - 3}{1 / \sqrt{2}} = \frac{y - 4}{1 / \sqrt{2}} = r = \pm 2 \sqrt{2}$
Hence, $x - 3 = y - 4 = \pm 2$
or $x = 5, 1$ and $y = 6, 2$
Hence, two of the vertices are $(1, 2)$ and $(5, 6)$
The other diagonal is parallel to the line $y = - x$ , so that its equation is
$\frac{x - 3}{- 1 / \sqrt{2}} = \frac{y - 4}{1 / \sqrt{2}} = r = \pm 2 \sqrt{2}$
Hence, the two vertices on this diagonal are (1,6) and (5,2)

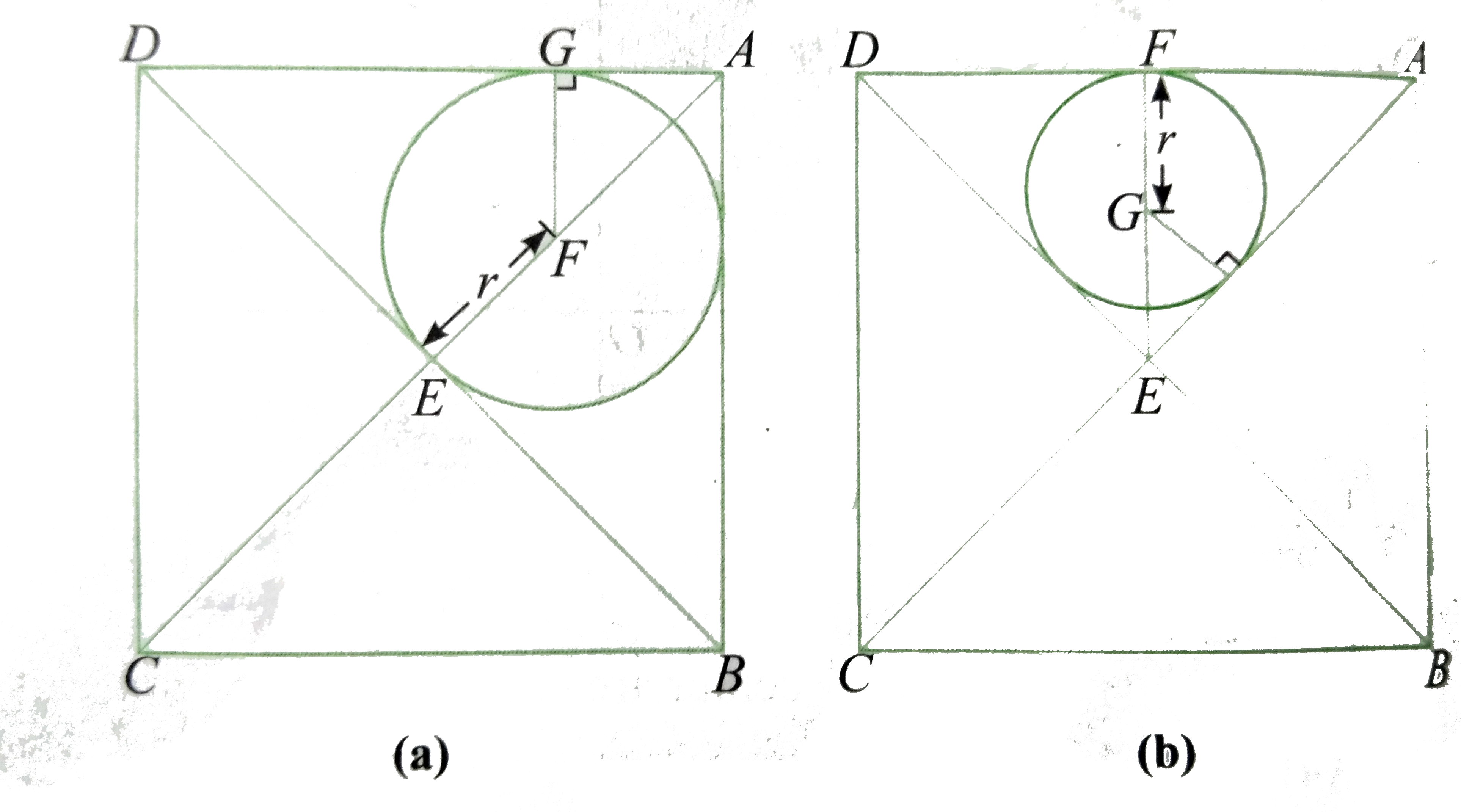
$A B = 4, A C = 4 \sqrt{2}$
$∴ A E = 2 \sqrt{2}$
In first figure, $E F + F A = A E$
or $r + \sqrt{2} r = 2 \sqrt{2}$
or $r = \frac{2 \sqrt{2}}{\sqrt{2} + 1} = 2 \sqrt{2} (\sqrt{2} - 1)$
In second figure, $E G + F G = E F$
or $\sqrt{2} r + r = 2$
or $r = \frac{2}{\sqrt{2} + 1} = 2 (\sqrt{2} - 1)$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If a vertex of a square is at the point $(1, - 1)$ and one of its sides lie along the line $3 x - 4 y - 17 = 0$ , then the area of the square is
A4 sq. units
B3 sq. units
C $\frac{1}{2}$ sq. units
D2 sq. units

CENGAGE ENGLISH-CIRCLE -Linked Comprehension Type (For Problem 1-3)

Home
Ask Doubt
Profile