A tangent to the ellipse x2+4y2=4 meets the ellipse x2+2y2=6 at P&Q.
The given ellipse are
x24+y21=1 (1)
and x26+y23=1 (2)
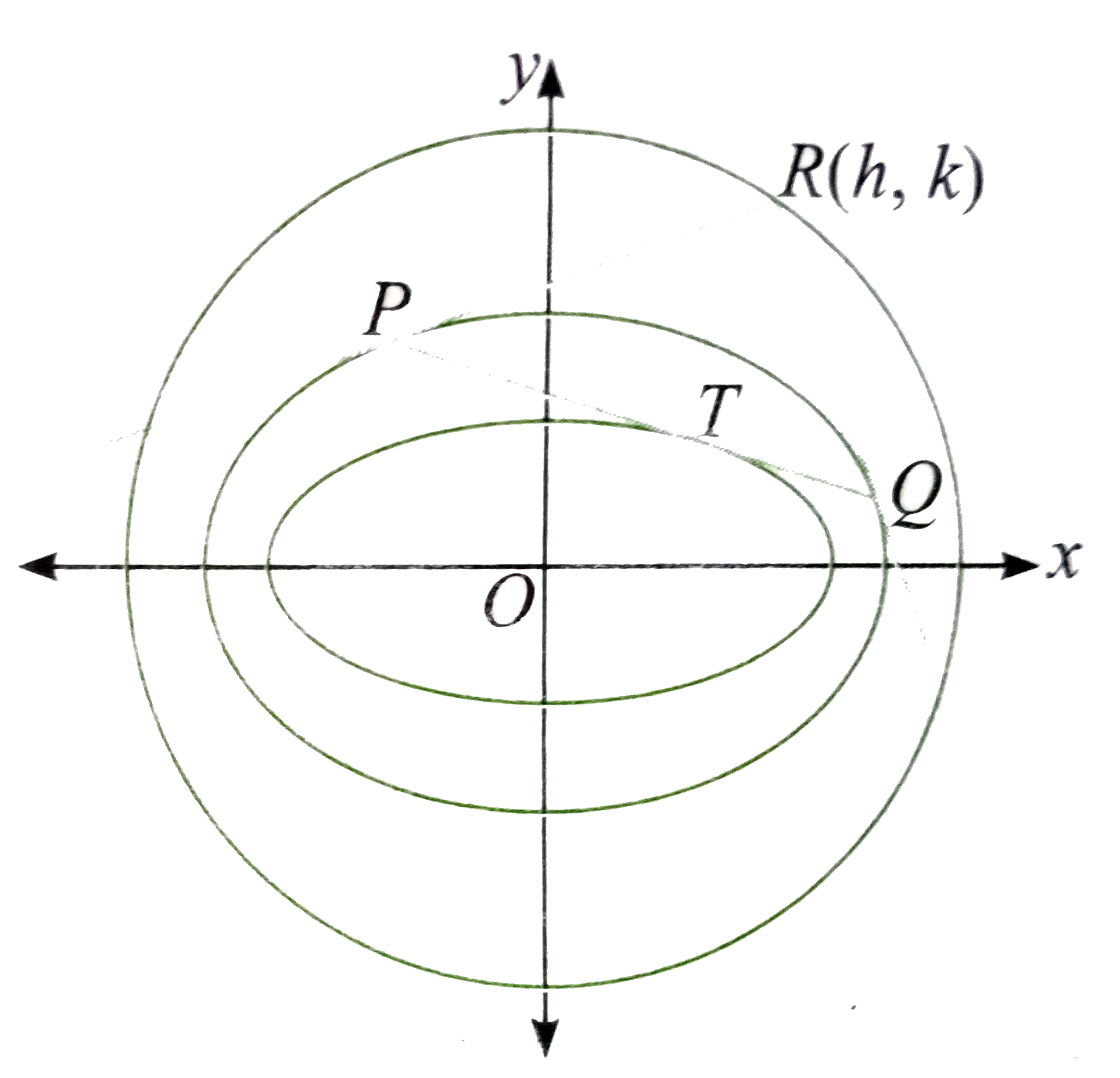
Then the equation of tangent to (1) at point T(2cosθ,sinθ) is given by
xcosθ2+ysinθ1=1 (3)
Let this tangent meet the ellipse (2)at P and Q . Let the tangents drawn to ellipse (2)at P and Q meet each other at R(h,k) .
Tehn PQ is the chord of contact of ellipse (2) with respect to teh point (R(h,k) and is given by
xh6+yk3=1
Clearly, (3) and (4) represent the same line and, hence should be identical.
Therefore, comapring the ratio of coefficients , we get
(cosθ)/2h/6=sinθk/3=11
or h=3cosθ,k=3sinθ
or h2+k2=9
Therfore, hte locus of (h,k) is x2+y2=9
Which is the director circle of he ellipse x26+y23=1
and we know that the director circle is the locus of the point of intersection of the tangents which are at right angle.
Thus, tangents at P and Q are perpendicular
Similar Questions
A tangent to the ellipse x2+4y2=4 meets the ellipse x2+2y2=6 at P and Q. The angle between the tangents at P and Q of the ellipse x2+2y2=6 is
View SolutionA tangent is drawn to the ellipse to cut the ellipse x2a2+y2b2=1 and to cut the ellipse x2c2+y2d2=1 at the points P and Q. If the tangents are at right angles, then the value of (a2c2)+(b2d2) is
View SolutionIf the ellipse x24+y2=1 meets the ellipse x2+y2a2=1 at four distinct points and a=b2−5b+7, then b does not lie in [4,5] (b) (−∞,2)∪(3,∞) (−∞,0) (d) [2,3]
View SolutionA tangent to the hyperbola x24−y21=1 meets ellipse x2+4y2=4 in two distinct points .
Then the locus of midpoint of this chord is
View SolutionA variable tangent to the circle x2+y2=1 intersects the ellipse x24+y22=1 at point P and Q. The lous of the point of the intersection of tangents to the ellipse at P and Q is another ellipse. Then find its eccentricity.
View SolutionHow many tangents to the circle x2+y2=3 are normal tothe ellipse x29+y24=1?
View SolutionThe locus of the point of intersection of the tangents at the extremities of the chords of the ellipse x2+2y2=6 which touch the ellipse x2+4y2=4, is x2+y2=4 (b) x2+y2=6 x2+y2=9 (d) None of these
View SolutionShow that the locus of the poles w.r.t. the parabola y2=4ax of tangents to x2−y2=a2 is the ellipse 4x2+y2=4a2.
View SolutionThe minimum length of intercept on any tangent to the ellipse x24+y29=1 cut by the circle x2+y2=25 is :
View SolutionIf the tangent to the ellipse x2+4y2=16 at the point 0 sanormal to the circle x2+y2−8x−4y=0 then θ is equal to
View Solution
