Find the positive integers p, q, r, s satisfying tan(π24)=(√p−√q)(√r−s)
6
7
8
9
The correct Answer is:C
Using tan2A=2tanA1−tan2A
tan7.5∘=sin15∘1+cos15∘
=sin15∘1+cos15∘×1−cos15∘1−cos15∘
=sin15∘(1−cos15∘)sin215∘
=1−cos15∘sin15∘
=1−√3+12√2√3−12√2
=2√2−√3−1√3−1
=2√2−√3−1√3−1×√3+1√3+1
=(2√2−√3−1)(√3+1)3−1
=2√6+2√2−4−2√32
=2(√6+√2−2−√3)2
=√3(√2−1)−√2(√2−1)
=(√3−√2)(√2−1)
Topper's Solved these Questions
- TRIGONOMETRIC RATIOS FOR COMPOUND, MULTIPLE, SUB-MULTIPLE ANGLES, AND TRANSFORMATION FORMULAS BOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC RATIOS FOR COMPOUND, MULTIPLE, SUB-MULTIPLE ANGLES, AND TRANSFORMATION FORMULAS EXERCISE - Multiple Correct Answers Type
6 Videos
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBOOK - CENGAGE ENGLISHCHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Matrix Match Type
1 Video
- VECTOR ALGEBRABOOK - CENGAGE ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - All Questions
532 Videos
Similar Questions
If p, q are prime positive integers, prove that √p+√q is an irrational number.
View SolutionA physical quantity A is dependent on other four physical quantities p,q,r and s as given by A=√pqr2s3. The percentage error of measurement in p,q,r and s are 1%,3%,0.5% and 0.33% respectively, then the maximum percentage error in A is
View SolutionThe positive integers p,q,&r are all primes if p2−q2=r, then find all possible values of r
View SolutionIf p,q, r are positive integers, find the maximum possible value of (p+q+r) if px−(x+r)=23x−15 .
View SolutionThe shaded region ,where P=(−1,0)Q=(−1+√2,√2)
R=(−1+√2,−√2),S=1(1,0) is represent by

View SolutionIf number of aldose, ketose, furanose and pyranose units present in maitose are p, q, r, s respectively. Find the value of p+q+r+s
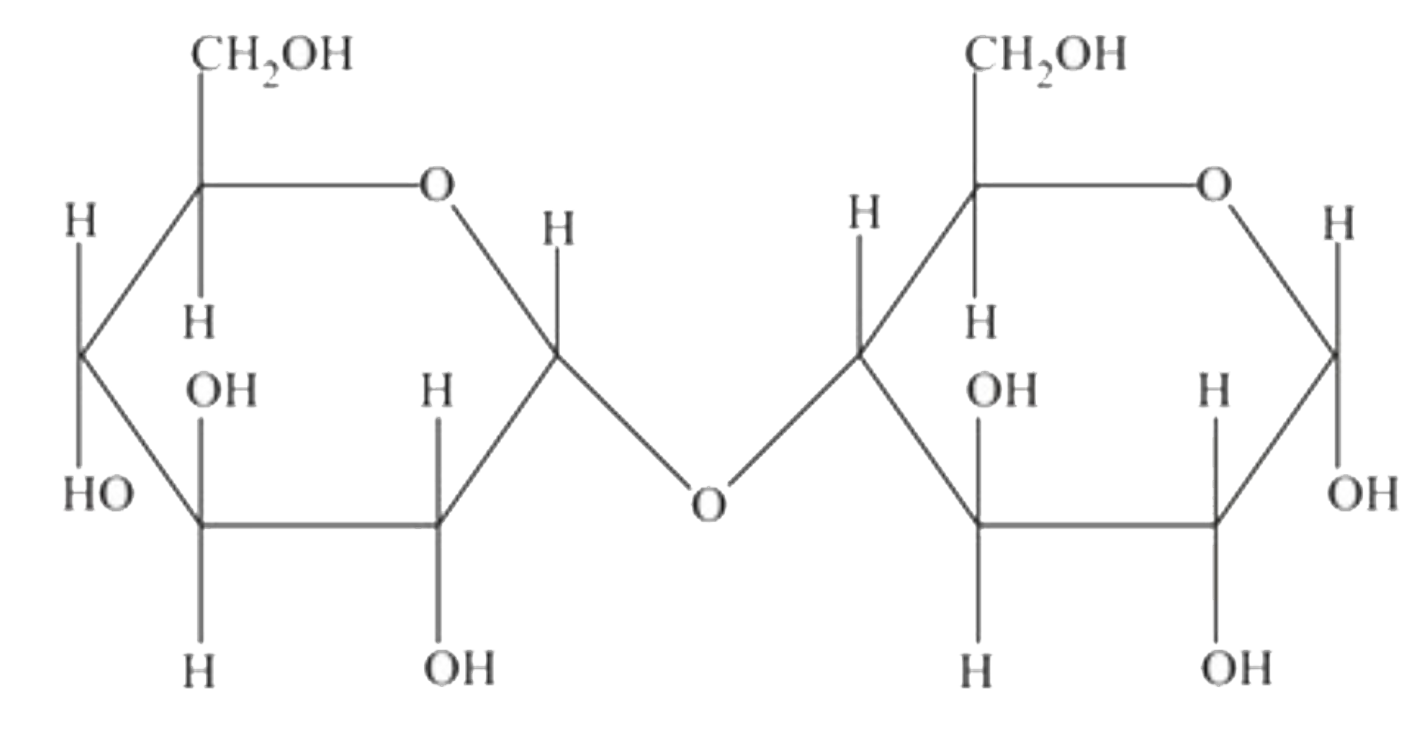
View SolutionIf P+Q=7π6, then find the value of (√3+tanP)×(√3+tanQ).
View SolutionStatement -1: There exists no A.P. whose three terms are √3,√5and√7.
Statement-2: If ap,aqandar are three distinct terms of an A.P., then ap−aqap−qr is a rational number.
View SolutionIn the given figure, PQR is an equilateral triangle and OSPT is square. If OT=2√2 units, find the equation of lines OT,OS,SP,QR,PR, and PQ.
View SolutionProve that the equation pcosx−qsinx=r admits solution for x only if −√p2+q2<r<√p2+q2
View Solution